2010年全国竞赛数学.doc
若实数a,b满足 ,则a的取值范围是 ( ).
,则a的取值范围是 ( ).
A.a≤ |
B.a≥4 | C.a≤ 或 a≥4 或 a≥4 |
D. ≤a≤4 ≤a≤4 |
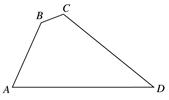
如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=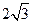 ,BC=
,BC=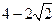 ,CD=
,CD= ,则AD边的长为( ).
,则AD边的长为( ).
A.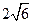 |
B.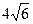 (第3题) |
C.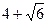 |
D.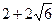 |
在一列数 ……中,已知
……中,已知 ,且当k≥2时,
,且当k≥2时,
(取整符号 表示不超过实数
表示不超过实数 的最大整数,例如
的最大整数,例如 ,
, ),则
),则 等于( ).
等于( ).
| A.1 | B.2 | C.3 | D.4 |
如图,在平面直角坐标系xOy中,等腰梯形ABCD的顶点坐标分别为A(1,1),B(2,-1),C(-2,-1),D(-1,1).y轴上一点P(0,2)绕点A旋转180°得点P1,点P1绕点B旋转180°得点P2,点P2绕点C旋转180°得点P3,点P3绕点D旋转180°得点P4,……,重复操作依次得到点P1,P2,…, 则点P2010的坐标是( ).
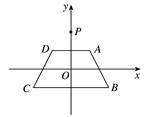
|
| A.(2010,2) | B.(2010,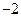 ) ) |
C.(2012,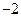 ) ) |
D.(0,2) |
一辆客车、一辆货车和一辆小轿车在一条笔直的公路上朝同一方向匀速行驶.在某一时刻,客车在前,小轿车在后,货车在客车与小轿车的正中间.过了10分钟,小轿车追上了货车;又过了5分钟,小轿车追上了客车;再过t分钟,货车追上了客车,则t= .
如图,在平面直角坐标系xOy中,多边形OABCDE的顶点坐标分别是O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).若直线l经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则直线l的函数表达式是 .


|
如图,射线AM,BN都垂直于线段AB,点E为AM上一点,过点A作BE的垂线AC分别交BE,BN于点F,C,过点C作AM的垂线CD,垂足为D.若CD=CF,则 .
. 
对于i=2,3,…,k,正整数n除以i所得的余数为i-1.若 的最小值
的最小值 满足
满足 ,则正整数
,则正整数 的最小值为 .
的最小值为 .
如图,△ABC为等腰三角形,AP是底边BC上的高,点D是线段PC上的一点,BE和CF分别是△ABD和△ACD的外接圆直径,连接EF. 求证:
|
 .
.

|
|
如图,抛物线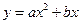 (a
(a 0)与双曲线
0)与双曲线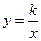 相交于点A,B. 已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).
相交于点A,B. 已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).
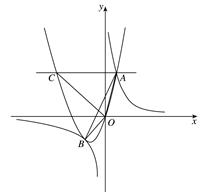
(1)求实数a,b,k的值;
(2)过抛物线上点A作直线AC∥x轴,交抛物线于另一点C,求所有满足△EOC∽△AOB的点E的坐标.
 ,则
,则 的值为( ).
的值为( ).



 -1,则2a3+7a2-2a-12 的值等于 .
-1,则2a3+7a2-2a-12 的值等于 .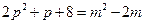 的所有素数p和正整数m.
的所有素数p和正整数m. 粤公网安备 44130202000953号
粤公网安备 44130202000953号