如图,设抛物线C1: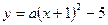 , C2:
, C2: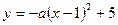 ,C1与C2的交点为A,
,C1与C2的交点为A,
B,点A的坐标是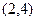 ,点B的横坐标是-2.
,点B的横坐标是-2.
(1)求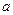 的值及点B的坐标;
的值及点B的坐标;
(2)点D在线段AB上,过D作x轴的垂线,垂足为点H,在DH的右侧作正三角形DHG. 过C2顶点M的直线记为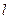 ,且
,且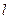 与x轴交于点N.
与x轴交于点N.
①若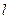 过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;
过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;
②若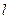 与△DHG的边DG相交,求点N的横坐标的取值范围.
与△DHG的边DG相交,求点N的横坐标的取值范围.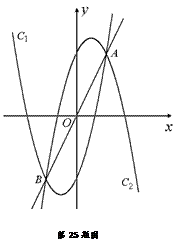
相关知识点
推荐套卷
如图,设抛物线C1: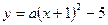 , C2:
, C2: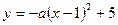 ,C1与C2的交点为A,
,C1与C2的交点为A,
B,点A的坐标是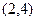 ,点B的横坐标是-2.
,点B的横坐标是-2.
(1)求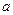 的值及点B的坐标;
的值及点B的坐标;
(2)点D在线段AB上,过D作x轴的垂线,垂足为点H,在DH的右侧作正三角形DHG. 过C2顶点M的直线记为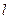 ,且
,且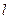 与x轴交于点N.
与x轴交于点N.
①若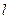 过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;
过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;
②若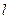 与△DHG的边DG相交,求点N的横坐标的取值范围.
与△DHG的边DG相交,求点N的横坐标的取值范围.