小明喜欢研究问题,他将一把三角板的直角顶点放在平面直角坐标系的原点 处,两条直角边与抛物线
处,两条直角边与抛物线 交于
交于 、
、 两点.
两点. (1)如左图,当
 时,则
时,则 = ;
= ;
(2)对同一条抛物线,当小明将三角板绕点
 旋转到如右图所示的位置时,过点
旋转到如右图所示的位置时,过点 作
作 轴于点
轴于点 ,测得
,测得 ,求出此时点
,求出此时点 的坐标;
的坐标;
(3)对于同一条抛物线,当小明将三角板绕点
 旋转任意角度时,他惊奇地发现,若三角板的两条直角边与抛物线有交点,则线段
旋转任意角度时,他惊奇地发现,若三角板的两条直角边与抛物线有交点,则线段
 总经过一个定点,请直接写出该定点的坐标.
总经过一个定点,请直接写出该定点的坐标.
如图,在Rt△ABC内有边长分别为a,b,c的三个正方形,则a,b,c满足的关系式为
| A.b=a+c | B.b=ac | C.b2=a2+c2 | D.b=2a=2c |
已知:在△ABC中AB=AC,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE=∠BDF,点M在线段DF上,∠ABE=∠DBM.如图1,当∠ABC=45°时,求证:AE=
 MD;
MD;
如图2,当∠ABC=60°时,则线段AE、MD之间的数量关系为: 。

在(2)的条件下延长BM到P,使MP=BM,连接CP,若AB=7,AE=
 ,求tan∠ACP的值.
,求tan∠ACP的值.
已知抛物线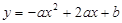 与x轴的一个交点为A(-1,0),与y轴正半轴交于点C.
与x轴的一个交点为A(-1,0),与y轴正半轴交于点C.
直接写出抛物线的对称轴,及抛物线与
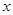 轴的另一个交点B的坐标;
轴的另一个交点B的坐标;当∠ACB=90°时,求抛物线的解析式;
抛物线上是否存在点M,使得△ABM和△ABC的面积相等(△ABM与△ABC重合除外)?若存在,请直接写出点M坐标;若不存在,请说明理由.
在第一象限内,抛物线上是否存在点N,使得△BCN的面积最大?若存在,求出这个最大值和点N坐标;若不存在,请说明理由.
如图1,Rt△ABC中,∠ACB=90°,AC=3,BC=4,点O是斜边AB上一动点,以OA为半径作⊙O与AC边交于点P,
当OA=
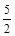 时,求点O到BC的距离
时,求点O到BC的距离如图2,当OA=
 时,求证:直线BC与⊙O相切;此时线段AP的长是多少?
时,求证:直线BC与⊙O相切;此时线段AP的长是多少?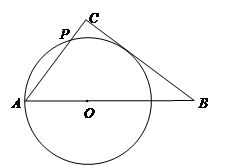
若BC边与⊙O有公共点,直接写出 OA
的取值范围;若CO平分∠ACB,则线段AP的长是多少?

如图1,正方形ABCD的边长为1,点E是AD边的中点,将△ABE沿BE翻折得到△FBE,延长BF交CD边于点G,则FG=DG,求出此时DG的值;
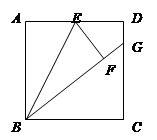
如图2,矩形ABCD中,AD>AB,AB=1,点E是AD边的中点,同样将△ABE沿BE翻折得到△FBE,延长BF交CD边于点G.
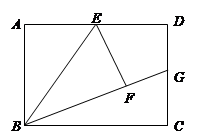
①证明:FG=DG;
②若点G恰是CD边的中点,求AD的值;
③若△ABE与△BCG相似,求AD的值.
在边长为10的正方形ABCD中,以AB为直径作半圆O,如图①,E是半圆上一动点,过点E作EF⊥AB,垂足为F,连结DE.
当DE=10时,求证:DE与圆O相切;
求DE的最长距离和最短距离;
如图②,建立平面直角坐标系,当DE =10时,试求直线DE的解析式.
如图,在直角坐标系中,抛物线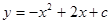 与
与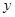 轴交于点D(0,3).
轴交于点D(0,3).
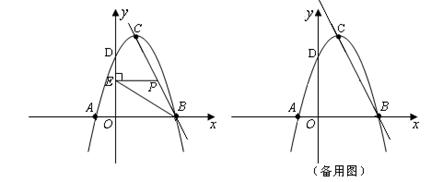
直接写出
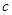 的值;
的值;
若抛物线与
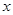 轴交于A、B两点(点B在点A的右边),顶点为C点,求直线BC的解析式;
轴交于A、B两点(点B在点A的右边),顶点为C点,求直线BC的解析式;
已知点P是直线BC上一个动点,
①当点P在线段BC上运动时(点P不与B、C重合),过点P作PE⊥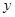 轴,垂足为E,连结BE.设点P的坐标为(
轴,垂足为E,连结BE.设点P的坐标为(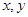 ),△PBE的面积为
),△PBE的面积为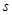 ,求
,求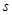 与
与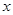 的函数关系式,写出自变量
的函数关系式,写出自变量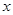 的取值范围,并求出
的取值范围,并求出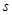 的最大值;
的最大值;
②试探索:在直线BC上是否存在着点P,使得以点P为圆心,半径为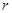 的⊙P,既与抛物线的对称轴相切,又与以点C为圆心,半径为1的⊙C相切?如果存在,试求
的⊙P,既与抛物线的对称轴相切,又与以点C为圆心,半径为1的⊙C相切?如果存在,试求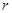 的值,并直接写出点P的坐标;如果不存在,请说明理由.
的值,并直接写出点P的坐标;如果不存在,请说明理由.
在平面直角坐标系中△ABC的边AB在x轴上,且OA>OB,以AB为直径的圆过点C,若C的坐标为(0,2),AB="5," A,B两点的横坐标XA,XB是关于X的方程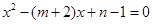 的两根:
的两根:
求m,n的值;
若∠ACB的平分线所在的直线
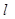 交x轴于点D,试求直线
交x轴于点D,试求直线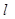 对应的一次函数的解析式;
对应的一次函数的解析式;过点D任作一直线
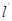 分别交射线CA,CB(点C除外)于点M,N,则
分别交射线CA,CB(点C除外)于点M,N,则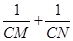 的值是否为定值,若是,求出定值,若不是,请说明理由
的值是否为定值,若是,求出定值,若不是,请说明理由
已知:如图①,在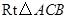 中,
中,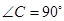 ,
,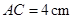 ,
,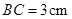 ,点
,点 由
由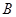 出发沿
出发沿 方向向点
方向向点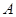 匀速运动,速度为1cm/s;点
匀速运动,速度为1cm/s;点 由
由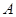 出发沿
出发沿 方向向点
方向向点 匀速运动,速度为2cm/s;连接
匀速运动,速度为2cm/s;连接 .若设运动的时间为
.若设运动的时间为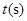 (
( ),解答下列问题
),解答下列问题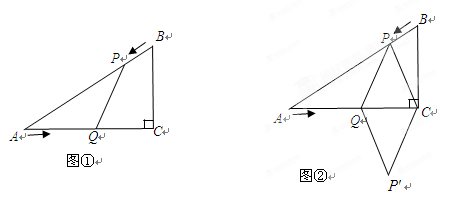
当
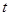 为何值时,
为何值时,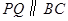 ?
?设
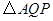 的面积为
的面积为 (
(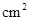 ),求
),求 与
与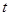 之间的函数关系式;
之间的函数关系式;是否存在某一时刻
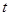 ,使线段
,使线段 恰好把
恰好把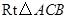 的周长和面积同时平分?若存在,求出此时
的周长和面积同时平分?若存在,求出此时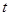 的值;若不存在,说明理由;
的值;若不存在,说明理由;如图②,连接
 ,并把
,并把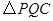 沿
沿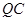 翻折,得到四边形
翻折,得到四边形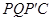 ,那么是否存在某一时刻
,那么是否存在某一时刻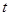 ,使四边形
,使四边形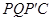 为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
、(本题12分)如图,设抛物线C1: , C2:
, C2: ,C1与C2的交点为A, B,点A的坐标是
,C1与C2的交点为A, B,点A的坐标是 ,点B的横坐标是-2.
,点B的横坐标是-2.
(1)求
 的值及点B的坐标;
的值及点B的坐标; (2)点D在线段AB上,过D作x轴的垂线,垂足为点H,在DH的右侧作正三角形DHG.记过C2顶点M的直线为
 ,且
,且 与x轴交于点N.
与x轴交于点N.
① 若 过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;
过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;
② 若 与△DHG的边DG相交,求点N的横坐标的取值范围.
与△DHG的边DG相交,求点N的横坐标的取值范围.
.如图,在平面直角坐标系 中,点
中,点 的坐标为
的坐标为 ,点
,点 在
在 轴的正半轴上,
轴的正半轴上, ,
, 为△
为△ 的中线,过
的中线,过 、
、 两点的抛物线
两点的抛物线 与
与 轴相交于
轴相交于 、
、 两点(
两点( 在
在 的左侧).
的左侧).
(1)求抛物线的解析式;
(2)等边△
 的顶点
的顶点 、
、 在线段
在线段 上,求
上,求 及
及 的长;
的长;(3)点
 为△
为△ 内的一个动点,设
内的一个动点,设 ,请直接写出
,请直接写出 的最小值,以及
的最小值,以及 取得最小值时,线段
取得最小值时,线段 的长.
的长.
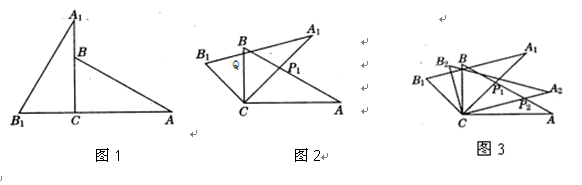
我们约定,若一个三角形(记为△A1)是由另一个三角形(记为△A)通过一次平移,或绕其任一边的中点旋转180°得到的,则称△A1是由△A复制的.以下的操作中每一个三角形只可以复制一次,复制过程可以一直进行下去.如图1,由△A复制出△A1,又由△A1复制出△A2,再由△A2复制出△A3,形成了一个大三角形,记作△B.以下各题中的复制均是由△A开始的,通过复制形成的多边形中的任意相邻两个小三角形(指与△A全等的三角形)之间既无缝隙也无重叠.
(1)图1中标出的是一种可能的复制结果,小明发现△A∽△B,其相似比为_________.在图1的基础上继续复制下去得到△C,若△C的一条边上恰有11个小三角形(指有一条边在该边上的小三角形),则△C中含有______个小三角形;
(2)若△A是正三角形,你认为通过复制能形成的正多边形是________;
(3)请你用两

 次旋转和一次平移复制形成一个四
次旋转和一次平移复制形成一个四 边形,在图2的方框内画出草图,并仿照图1作出标记.
边形,在图2的方框内画出草图,并仿照图1作出标记.
如图,在Rt△ABC中,∠C=90°,AC=BC=4cm,点D为AC边上一点,且AD=3cm,动点E从点A出发,以1cm/s的速度沿线段AB向终点B运动,运动时间为x s.作∠DEF=45°,与边BC相交于点F.设BF长为ycm.(1)当x= ▲ s时,DE⊥AB;
(2)求在点E运动过程中,y与x之间的函数关系式及点F运动路线的长;
(3)当△BEF为等腰三角形时,求x的值.

将两块全等的三角板如图1摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°。(1)将图1中△A1B1C绕点C顺时针旋转45°得图2,点
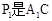 与AB的交点,点Q是
与AB的交点,点Q是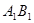 与BC的交点,求证:
与BC的交点,求证: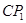 =
=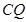 ;
;(2)在图2中,若AP1=
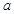 ,则CQ等于多少?
,则CQ等于多少?(3)将图2中△
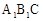 绕点C顺时针旋转到△
绕点C顺时针旋转到△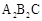 (如图3),点
(如图3),点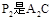 与AP1的交点.当旋转角为多少度时,有△A P1C∽△CP1P2? 这时线段
与AP1的交点.当旋转角为多少度时,有△A P1C∽△CP1P2? 这时线段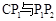 之间存在一个怎样的数量关系?.
之间存在一个怎样的数量关系?.