[北京]2011-2012学年北京市丰台区九年级上学期期末考试数学卷
⊙O1和⊙O2的半径分别为3cm和5cm,若O1O2=8cm,则⊙O1和⊙O2的位置关系是
| A.外切 | B.相交 | C.内切 | D.内含 |
若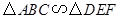 ,相似比为1∶2,且△ABC的面积为4,则△DEF的面积为
,相似比为1∶2,且△ABC的面积为4,则△DEF的面积为
| A.16 | B.8 | C.4 | D.2 |
如图,⊙O的半径为5,AB为弦,半径OC⊥AB,垂足为点E,若CE=2,则AB的长是 
| A.4 | B.6 | C.8 | D.10 |
. 如图,若点P在反比例函数 的图象上,过点P作PM⊥x轴于点
的图象上,过点P作PM⊥x轴于点 ,PN⊥y轴于点N,若矩形PMON的面积为6,则
,PN⊥y轴于点N,若矩形PMON的面积为6,则 的值是
的值是
| A.-3 | B.3 | C.-6 | D.6 |
如图,在矩形ABCD中,AB=4cm,AD=2cm,动点M自点A出发沿A→B的方向,以每秒1cm的速度运动,同时动点N自点A出发沿A→D→C的方向以每秒2cm的速度运动,当点N到达点C时,两点同时停止运动,设运动时间为x(秒),△AMN的面积为y(cm2),则下列图象中能反映y与x之间的函数关系的是

如图,在△ABC中,点D、E分别在AB、AC边上,且 DE∥BC,若AD∶DB=3∶2,AE=6,则EC的长等于 .
如图,△ABC内接于⊙O,AB是⊙O的直径,∠ABC=20°,点D是弧 CAB上一点,若∠ABC=20°,则∠D的度数是______.
CAB上一点,若∠ABC=20°,则∠D的度数是______.
已知二次函数y=ax2+bx+c,若x与y的部分对应值如下表:
| x |
0 |
1 |
2 |
3 |
| y |
-5 |
-8 |
-9 |
-8 |
则当x=4时,y= .
我们定义:“四个顶点都在三角形边上的正方形是三角形的内接正方形” .
已知:在Rt△ABC中,∠C=90°,AC=6,BC=3.
(1)如图,四边形CDEF是△ABC的内接正方形,则正方形CDEF的边长a1是 ;
(2)如图,四边形DGHI是(1)中△EDA的内接正方形,则第2个正方形DGHI的边长a2= ;继续在图2中的△HGA中按上述方法作第3个内接正方形;…以此类推,则第n个内接正方形的边长an= .(n为正整数) 
已知二次函数 .
.(1)求出这个函数图象的对称轴和顶点坐标;
(2)求出这个函数图象与
 轴、y轴的交点坐标.
轴、y轴的交点坐标.
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,联结BD,过点C作CE⊥BD于交AB于点E,垂足为点H,若AD=2,AB=4,求sin∠BCE.

.已知:在平面直角坐标系xOy中,将直线 绕点O顺时针旋转90°得到直线l,反比例函数
绕点O顺时针旋转90°得到直线l,反比例函数 的图象与直线l的一个交点为A(a,2),试确定反比例函数的解析式.
的图象与直线l的一个交点为A(a,2),试确定反比例函数的解析式.
如图,天空中有一个静止的热气球A,从地面点B测得A的仰角为30°,从地面点C测得A的仰角为60°.已知BC=50m,点A和直线BC在同一垂直平面上,求热气球离地面的高度.
如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,以AB上一点O为圆心,AD为弦作⊙O. (1)求证:BC为⊙O的切线;
(2)若AC= 6,tanB=
 ,求⊙O的半径.
,求⊙O的半径.
某工厂设计了一款产品,成本为每件20元.投放市场进行试销,得到如下数据:
售价 (元∕件) (元∕件) |
…… |
30 |
40 |
50 |
60 |
…… |
日销售量 (件) (件) |
…… |
500 |
400 |
300 |
200 |
…… |
(1)若日销售量
 (件)是售价
(件)是售价 (元∕件)的一次函数,求这个一次函数的解析式;
(元∕件)的一次函数,求这个一次函数的解析式;(2)设这个工厂试销该产品每天获得的利润为W(元),当售价定为每件多少元时,工厂每天获得的利润最大?最大利润是多少元?
小明喜欢研究问题,他将一把三角板的直角顶点放在平面直角坐标系的原点 处,两条直角边与抛物线
处,两条直角边与抛物线 交于
交于 、
、 两点.
两点. (1)如左图,当
 时,则
时,则 = ;
= ;
(2)对同一条抛物线,当小明将三角板绕点
 旋转到如右图所示的位置时,过点
旋转到如右图所示的位置时,过点 作
作 轴于点
轴于点 ,测得
,测得 ,求出此时点
,求出此时点 的坐标;
的坐标;
(3)对于同一条抛物线,当小明将三角板绕点
 旋转任意角度时,他惊奇地发现,若三角板的两条直角边与抛物线有交点,则线段
旋转任意角度时,他惊奇地发现,若三角板的两条直角边与抛物线有交点,则线段
 总经过一个定点,请直接写出该定点的坐标.
总经过一个定点,请直接写出该定点的坐标.
在平面直角坐标系xOy中,抛物线 与直线y=x-1交于A(-1,a)、B(b,0)两点,与y轴交于点C.
与直线y=x-1交于A(-1,a)、B(b,0)两点,与y轴交于点C.(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)点
 是x轴上的一个动点.过点P作x轴的垂线交直线AB于点M,交抛物线于点N.当点M位于点N的上方时,直接写出t的取值范围.
是x轴上的一个动点.过点P作x轴的垂线交直线AB于点M,交抛物线于点N.当点M位于点N的上方时,直接写出t的取值范围.
在Rt△ABC中,∠ACB=90 ,AC=BC,CD⊥AB于点D,点E为AC边上一点,联结BE交CD于点F,过点E作EG⊥BE交AB于点G,
,AC=BC,CD⊥AB于点D,点E为AC边上一点,联结BE交CD于点F,过点E作EG⊥BE交AB于点G,如图1,当点E为AC中点时,线段EF与EG的数量关系是 ;
如图2,当
 ,探究线段EF与EG的数量关系并且证明;
,探究线段EF与EG的数量关系并且证明;如图3,当
 ,线段EF与EG的数量关系是 .
,线段EF与EG的数量关系是 .
 ,则下列比例式成立的是
,则下列比例式成立的是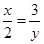



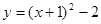 的最小值是
的最小值是



 ,则∠A=__________.
,则∠A=__________.
 轴上有一动点M,那么在两条抛物线C1、C2上是否存在点N,使得以点O、P、M、N为顶点的四边形是平行四边形(OP为一边)?若存在,求出点N的坐标;若不存在,请说明理由.
轴上有一动点M,那么在两条抛物线C1、C2上是否存在点N,使得以点O、P、M、N为顶点的四边形是平行四边形(OP为一边)?若存在,求出点N的坐标;若不存在,请说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号