[福建]2011-2012学年福建南安市初三学业质量检查数学试卷
如图,射线BA、CA交于点A,连接BC,已知AB=AC,∠B=40°,
那么 的值是( ).
的值是( ).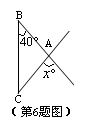
A.40 B.60 C.80 D.100
如图,E、F分别是正方形ABCD的边AD、CD上的点,且DE=CF,
AF、BE相交于点O,下列结论①AF=BE;②AF⊥BE;③ AO=OF;
④S△AOB=S四边形DEOF中,错误的有( ).
A.1个 B.2个 C.3个 D.4个
老师对甲、乙两同学最近5次数学测试成绩进行统计,发现两人
的平均成绩相同,但甲同学的方差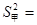 5,乙同学的方差
5,乙同学的方差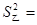 4.2,
4.2,
则 的成绩较稳定(填“甲”或“乙”).
如图,在等腰梯形ABCD中,AB//CD,AD=BC,AB=5,
CD=2,∠A=60°,则腰AD的长为 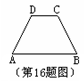
如图,在半径为 ,圆心角等于45°的扇形AOB内部作一个矩形CDEF,使点C在OA上,点D、E在OB上,点F在弧AB上,且DE=2CD,则:
,圆心角等于45°的扇形AOB内部作一个矩形CDEF,使点C在OA上,点D、E在OB上,点F在弧AB上,且DE=2CD,则:
弧AB的长是(结果保留
 )
) 图中阴影部分的面积为(结果保留
 ) .
) .
在学校组织的“喜迎建党90周年”的知识竞赛中,
每班参加比赛的人数相同,成绩分为A、B、C、D四个
等级,其中相应等级的得分依次记为100分、90分、
80分、70分.学校将某年级的一班和二班的成绩整理
并绘制成如右边的两个统计图:
请你根据图表提供的信息解答下列问题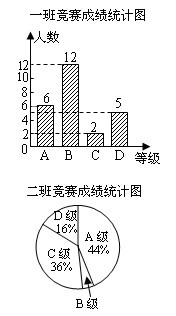
此次竞赛中二班参加比赛的人数为 ;
并将下面的表格补充完整
| |
众数 |
中位数 |
平均数 |
| 一班 |
|
90 |
|
| 二班 |
100 |
|
87.6 |
请你从B级以上(包括B级)的人数的角度来比较
一班和二班的成绩
如图,已知平行四边形ABCD的对角线AC的垂直
平分线与边AD、BC分别交于E、F两点,垂足是点O.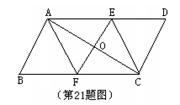
求证:△AOE≌△COF;
问:四边形AFCE是什么特殊的四边形?
(直接写出结论,不需要证明)
一个不透明的口袋中装有红、黄、绿三种颜色的小球(它们除颜色不同外其余都相同),其中红球2个,黄球1个,从中任意摸出1球是红球的概率是 .
.求口袋中绿球的个数;
第一次从袋中任意摸出1球(不放回),第二次再任意摸出1球,请你用画树状图或列表的方法表示所有等可能的结果,并求两次都摸到红球的概率.
如图,在 的正方形网格中,每个小正方形的边长
的正方形网格中,每个小正方形的边长
都是1,△ABC的三个顶点都在格点(即小正方形的顶点)上画出线段AC平移后的线段BD,其平移方向为射线AB
的方向,平移的距离为线段AB的长求sin∠DBC的值.
李明到某零件加工厂作社会调查,了解到该工厂为了激励工人的工作积极性,实行“月总收入=基本工资 计件奖金”的方法,并获
计件奖金”的方法,并获
得如右表信息.假设生产每件零件奖励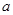 元,每个
元,每个
工人月基本工资都是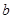 元
元
求
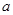 、
、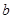 的值;
的值;若工人小王某月的总收入不低于1800元,
那么小王当月至少要生产零件多少件?
在平面直角坐标系中,把矩形OABC的边OA、OC
分别放在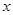 轴和
轴和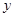 轴的正半轴上,已知OA
轴的正半轴上,已知OA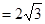 ,OC
,OC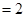
直接写出A、B、C三点的坐标
将矩形OABC绕点O逆时针旋转
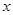 °,得到矩形OA1B1C1,
°,得到矩形OA1B1C1,
其中点A的对应点为点A1.
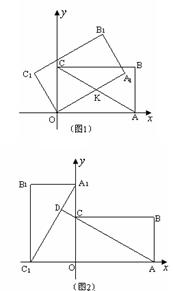
①当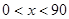 时,设AC交OA1于点K(如图1),
时,设AC交OA1于点K(如图1),
若△OAK为等腰三角形,请直接写出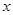 的值;
的值;
②当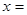 90时(如图2),延长AC交A1C1于点D,
90时(如图2),延长AC交A1C1于点D,
求证:AD⊥A1C1;
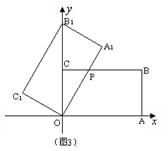
③当点B1落在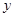 轴正半轴上时(如图3),设BC
轴正半轴上时(如图3),设BC
与OA1交于点P,求过点P的反比例函数的解析式;
并探索:该反比例函数的图象是否经过矩形OABC
的对称中心?请说明理由.
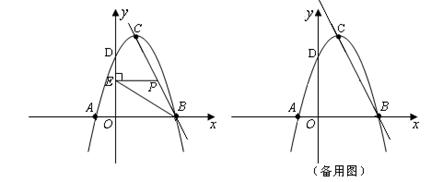
如图,在直角坐标系中,抛物线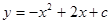 与
与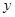 轴交于点D(0,3).
轴交于点D(0,3).
直接写出
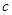 的值;
的值;
若抛物线与
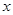 轴交于A、B两点(点B在点A的右边),顶点为C点,求直线BC的解析式;
轴交于A、B两点(点B在点A的右边),顶点为C点,求直线BC的解析式;
已知点P是直线BC上一个动点,
①当点P在线段BC上运动时(点P不与B、C重合),过点P作PE⊥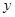 轴,垂足为E,连结BE.设点P的坐标为(
轴,垂足为E,连结BE.设点P的坐标为(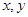 ),△PBE的面积为
),△PBE的面积为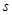 ,求
,求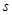 与
与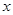 的函数关系式,写出自变量
的函数关系式,写出自变量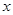 的取值范围,并求出
的取值范围,并求出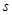 的最大值;
的最大值;
②试探索:在直线BC上是否存在着点P,使得以点P为圆心,半径为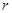 的⊙P,既与抛物线的对称轴相切,又与以点C为圆心,半径为1的⊙C相切?如果存在,试求
的⊙P,既与抛物线的对称轴相切,又与以点C为圆心,半径为1的⊙C相切?如果存在,试求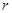 的值,并直接写出点P的坐标;如果不存在,请说明理由.
的值,并直接写出点P的坐标;如果不存在,请说明理由.


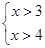 的解集的情况为( ).
的解集的情况为( ).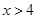
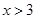
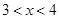

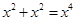
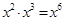

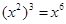
 、
、 相交于点O,若∠1=50°,则∠2= °.
相交于点O,若∠1=50°,则∠2= °.
 的解是
的解是  ,则它的图象经过第一象限、原点和第 象限
,则它的图象经过第一象限、原点和第 象限

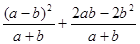 ,其中
,其中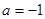 ,
,
 的解是 .
的解是 .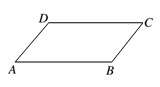
 粤公网安备 44130202000953号
粤公网安备 44130202000953号