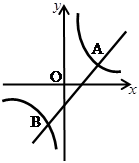(1)如图1, 是正方形 边 上的一点,连接 、 ,将 绕点 逆时针旋转 ,旋转后角的两边分别与射线 交于点 和点 .
①线段 和 的数量关系是 ;
②写出线段 , 和 之间的数量关系.
(2)当四边形 为菱形, ,点 是菱形 边 所在直线上的一点,连接 、 ,将 绕点 逆时针旋转 ,旋转后角的两边分别与射线 交于点 和点 .
①如图2,点 在线段 上时,请探究线段 、 和 之间的数量关系,写出结论并给出证明;
②如图3,点 在线段 的延长线上时, 交射线 于点 ,若 , ,直接写出线段 的长度.

在矩形 中,连结 ,点 从点 出发,以每秒1个单位的速度沿着 的路径运动,运动时间为 (秒 .过点 作 于点 ,在矩形 的内部作正方形 .
(1)如图,当 时,
①若点 在 的内部,连结 、 ,求证: ;
②当 时,设正方形 与 的重叠部分面积为 ,求 与 的函数关系式;
(2)当 , 时,若直线 将矩形 的面积分成 两部分,求 的值.

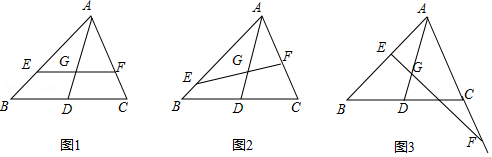
在 中,已知 是 边的中点, 是 的重心,过 点的直线分别交 、 于点 、 .
(1)如图1,当 时,求证: ;
(2)如图2,当 和 不平行,且点 、 分别在线段 、 上时,(1)中的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.
(3)如图3,当点 在 的延长线上或点 在 的延长线上时,(1)中的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.
在 的方格纸中,点 , , 都在格点上,按要求画图:
(1)在图1中找一个格点 ,使以点 , , , 为顶点的四边形是平行四边形.
(2)在图2中仅用无刻度的直尺,把线段 三等分(保留画图痕迹,不写画法).

在 的方格纸中,点 , , 都在格点上,按要求画图:
(1)在图1中找一个格点 ,使以点 , , , 为顶点的四边形是平行四边形.
(2)在图2中仅用无刻度的直尺,把线段 三等分(保留画图痕迹,不写画法).

如图, 一座钢结构桥梁的框架是 ,水平横梁 长 18 米, 中柱 高 6 米, 其中 是 的中点, 且 .
(1) 求 的值;
(2) 现需要加装支架 、 ,其中点 在 上, ,且 ,垂足为点 ,求支架 的长 .

数学活动课上,张老师引导同学进行如下探究:
如图1,将长为 的铅笔 斜靠在垂直于水平桌面 的直尺 的边沿上,一端 固定在桌面上,图2是示意图.
活动一
如图3,将铅笔 绕端点 顺时针旋转, 与 交于点 ,当旋转至水平位置时,铅笔 的中点 与点 重合.

数学思考
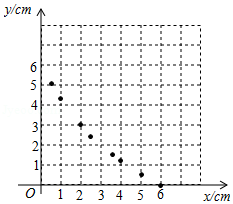
(1)设 ,点 到 的距离 .
①用含 的代数式表示: 的长是 , 的长是 ;
② 与 的函数关系式是 ,自变量 的取值范围是 .
活动二
(2)①列表:根据(1)中所求函数关系式计算并补全表格
|
|
6 |
5 |
4 |
3.5 |
3 |
2.5 |
2 |
1 |
0.5 |
0 |
|
|
0 |
0.55 |
1.2 |
1.58 |
|
2.47 |
3 |
4.29 |
5.08 |
|
②描点:根据表中数值,继续描出①中剩余的两个点 .
③连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象.
数学思考
(3)请你结合函数的图象,写出该函数的两条性质或结论.
如图,已知一次函数 的图象与反比例函数
的图象与反比例函数 的图象交于A,B两点,
的图象交于A,B两点,
且点A的横坐标和点B的纵坐标都是-2,
求:(1)一次函数的解析式;
(2)△AOB的面积.
已知反比例函数 的图象经过点A(-2,3).
的图象经过点A(-2,3).
(1)求出这个反比例函数的解析式;
(2)经过点A的正比例函数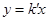 的图象与反比例函数图象还有其他的交点吗?若有,求出交点坐标;若没有,说明理由.
的图象与反比例函数图象还有其他的交点吗?若有,求出交点坐标;若没有,说明理由.
已知反比例函数y1=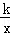 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2).
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2).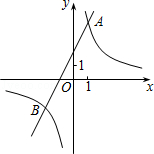
(1)求这两个函数的关系式;
(2)观察图象,直接写出使y1>y2成立的自变量x的取值范围.
已知:如图,在平面直角坐标系 中,直线AB分别与
中,直线AB分别与 轴交于点B、A,与反比例函数的图象分别交于点C、D,
轴交于点B、A,与反比例函数的图象分别交于点C、D,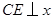 轴于点E,
轴于点E,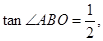
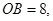
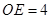 .求该反比例函数的解析式.
.求该反比例函数的解析式.
如图,在直角梯形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0),(2,6),点D为AB上一点,且BD=2AD,曲线 (k>0)经过点D,交BC于点E.
(k>0)经过点D,交BC于点E.
(1)求曲线的解析式;
(2)求四边形ODBE的面积.
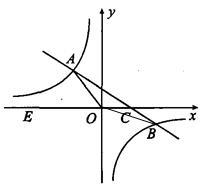
如图在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=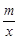 (m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=
(m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=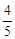 .
.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)直接写出不等式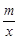 ﹤kx+b的x的取值范围.
﹤kx+b的x的取值范围.
如图,已知一次函数 与反比例函数
与反比例函数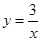 的图象交于A,B两点.求A,B两点的坐标.
的图象交于A,B两点.求A,B两点的坐标.