如图,在四边形ABCD中, ,将△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE,若 , ,则BD= (提示:可连接BE)

一副三角板如图放置,将三角板 ADE绕点 A逆时针旋转α(0°<α<90°),使得三角板 ADE的一边所在的直线与 BC垂直,则α的度数为 .

如图,在△ ABC中,∠ CAB=55°,∠ ABC=25°,在同一平面内,将△ ABC绕 A点逆时针旋转70°得到△ ADE,连接 EC,则tan∠ DEC的值是 .

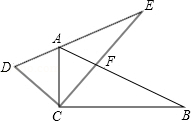
如图,在Rt△ ACB中,∠ ACB=90°, AC= BC, D是 AB上的一个动点(不与点 A, B重合),连接 CD,将 CD绕点 C顺时针旋转90°得到 CE,连接 DE, DE与 AC相交于点 F,连接 AE.下列结论:
①△ ACE≌△ BCD;
②若∠ BCD=25°,则∠ AED=65°;
③ DE 2=2 CF• CA;
④若 AB=3 , AD=2 BD,则 AF= .
其中正确的结论是 .(填写所有正确结论的序号)

两个全等的三角尺重叠放在△ACB的位置,将其中一个三角尺绕着点C按逆时针方向旋转至△DCE的位置,使点A恰好落在边DE上,AB与CE相交于点F.已知∠ACB=∠DCE=90°,∠B=30°,AB=8cm,则CF= cm.
如图所示,正方形ABCD对角线AC所在直线上有一点O,OA=AC=2,将正方形绕O点顺时针旋转60°,在旋转过程中,正方形扫过的面积是 .

如图,在Rt△ ABC中,∠ C=90°, AC=3, BC=4,把△ ABC绕 AB边上的点 D顺时针旋转90°得到△ A′ B′ C′, A′ C′交 AB于点 E,若 AD= BE,则△ A′ DE的面积是 .

如图,在Rt△ ABC中,∠ B=90°, AB= BC=2,将△ ABC绕点 C顺时针旋转60°,得到△ DEC,则 AE的长是 .

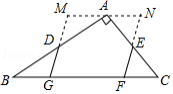
如图,在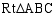 中,
中,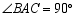 ,
,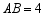 ,
,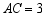 ,点
,点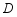 、
、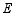 分别是
分别是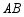 、
、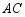 的中点,点
的中点,点 、
、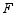 在
在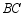 边上(均不与端点重合),
边上(均不与端点重合),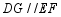 .将
.将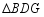 绕点
绕点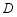 顺时针旋转
顺时针旋转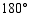 ,将
,将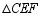 绕点
绕点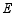 逆时针旋转
逆时针旋转 ,拼成四边形
,拼成四边形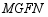 ,则四边形
,则四边形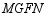 周长
周长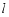 的取值范围是 .
的取值范围是 .
如图,正方形OABC的边长为2,以O为圆心,EF为直径的半圆经过点A,连接AE,CF相交于点P,将正方形OABC从OA与OF重合的位置开始,绕着点O逆时针旋转90°,交点P运动的路径长是 .

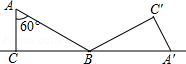
如图,△ABC中,∠C=90°,∠A=60°, .将△ABC沿直线CB向右作无滑动滚动一次,则点C经过的路径长是 .
如图,四边形 ABCO是平行四边形, OA=2, AB=6,点 C在 x轴的负半轴上,将▱ ABCO绕点 A逆时针旋转得到▱ ADEF, AD经过点 O,点 F恰好落在 x轴的正半轴上,若点 D在反比例函数 y= ( x<0)的图象上,则 k的值为 .

如图,在 中, , .将 绕点 逆时针旋转 ,得到△ ,则 边的中点 与其对应点 的距离是 .
