我们在学完“平移、轴对称、旋转”三种图形的变化后,可以进行进一步研究,请根据示例图形,完成下表.
图形的变化 |
示例图形 |
与对应线段有关的结论 |
与对应点有关的结论 |
平移 |
|
(1) |
|
轴对称 |
|
(2) |
(3) |
旋转 |
|
;对应线段 和 所在的直线相交所成的角与旋转角相等或互补. |
(4) |
在平面直角坐标系 中,将一块含有 角的直角三角板如图放置,直角顶点 的坐标为 ,顶点 的坐标为 ,顶点 恰好落在第一象限的双曲线上,现将直角三角板沿 轴正方向平移,当顶点 恰好落在该双曲线上时停止运动,则此时点 的对应点 的坐标为

A. , B. C. , D.
已知点 的坐标为 ,点 的坐标为 .将线段 沿某一方向平移后,点 的对应点的坐标为 .则点 的对应点的坐标为
A. B. C. D.
如图,在正方形网格(每个小正方形的边长都是 中,若将 沿 的方向平移 长,得 、 的对应点分别为 、 ,则 长为

A.1B.2C. D.3
如图, 沿着 方向平移得到△ ,点 是直线 上任意一点,若 ,△ 的面积分别为 , ,则下列关系正确的是
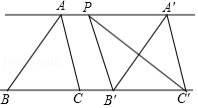
A. B. C. D.
如图,在平面直角坐标系中,直线y=2x与反比例函数 在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数 在第一象限内的图象交于点P,且△POA的面积为2.
(1)求k的值.
(2)求平移后的直线的函数解析式.

如图,在 中, .将 沿着 方向平移得到 ,其中点 在边 上, 与 相交于点 .
(1)求证: 为等腰三角形;
(2)连接 、 、 ,当点 在什么位置时,四边形 为矩形,并说明理由.

如图,把三角板的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,则顶点 平移的距离 .

对于平面图形上的任意两点 , ,如果经过某种变换得到新图形上的对应点 , ,保持 ,我们把这种变换称为“等距变换”,下列变换中不一定是等距变换的是
A.平移B.旋转C.轴对称D.位似
在 中, , ,点 、 ,点 在第一象限内,双曲线 经过点 .将 沿 轴向上平移 个单位长度,使点 恰好落在双曲线上,则 的值为

A.2B. C.3D.
如图,△ABC中,AB=AC,BC=12cm,点D在AC上,DC=4cm.将线段DC沿着CB的方向平移7cm得到线段EF,点E,F分别落在边AB,BC上,则△EBF的周长为 cm.

如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件能够判定四边形ACED为菱形的是( )

A.AB=BCB.AC=BCC.∠B=60°D.∠ACB=60°