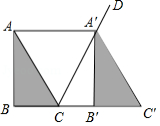
如图,在正方形网格(每个小正方形的边长都是 中,若将 沿 的方向平移 长,得 、 的对应点分别为 、 ,则 长为

A.1B.2C. D.3
如图,在 中, .将 沿着 方向平移得到 ,其中点 在边 上, 与 相交于点 .
(1)求证: 为等腰三角形;
(2)连接 、 、 ,当点 在什么位置时,四边形 为矩形,并说明理由.

如图,在 中, , , .线段 由线段 绕点 按逆时针方向旋转 得到, 由 沿 方向平移得到,且直线 过点 .
(1)求 的大小;
(2)求 的长.

小军同学在网格纸上将某些图形进行平移操作,他发现平移前后的两个图形所组成的图形可以是轴对称图形.如图所示,现在他将正方形 从当前位置开始进行一次平移操作,平移后的正方形顶点也在格点上,则使平移前后的两个正方形组成轴对称图形的平移方向有

A.3个B.4个C.5个D.无数个
如图,菱形 的边长为 , ,将该菱形沿 方向平移 得到四边形 , 交 于点 ,则点 到 的距离为 .
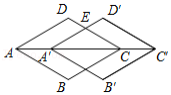
如图,在菱形 中, ,它的一个顶点 在反比例函数 的图象上,若将菱形向下平移2个单位,点 恰好落在函数图象上,则反比例函数解析式为

A. B. C. D.
已知 的三个顶点为 , , ,将 向右平移 个单位后, 某一边的中点恰好落在反比例函数 的图象上,则 的值为 .
如图,将 向右平移 得到 ,如果 的周长是 ,那么四边形 的周长是

A. B. C. D.
如图,把三角板的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,则顶点 平移的距离 .

对于平面图形上的任意两点 , ,如果经过某种变换得到新图形上的对应点 , ,保持 ,我们把这种变换称为“等距变换”,下列变换中不一定是等距变换的是
A.平移B.旋转C.轴对称D.位似
如图,将 沿着射线 方向平移至△ ,使点 落在 的外角平分线 上,连接 .
(1)判断四边形 的形状,并说明理由;
(2)在 中, , , ,求 的长.