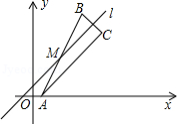
在 中, , ,点 、 ,点 在第一象限内,双曲线 经过点 .将 沿 轴向上平移 个单位长度,使点 恰好落在双曲线上,则 的值为

A.2B. C.3D.
如图,将 沿 边上的中线 平移到△ 的位置.已知 的面积为16,阴影部分三角形的面积9.若 ,则 等于

| A. |
2 |
B. |
3 |
C. |
4 |
D. |
|
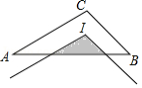
如图,点 为 的内心, , , ,将 平移使其顶点与 重合,则图中阴影部分的周长为
| A. |
4.5 |
B. |
4 |
C. |
3 |
D. |
2 |
如图1,在 中, 于点 , 的垂直平分线交 于点 ,交 于点 , , , .
(1)如图2,作 于点 ,交 于点 ,将 沿 方向平移,得到△ ,连接 .
①求四边形 的面积;
②直线 上有一动点 ,求 周长的最小值.
(2)如图3,延长 交 于点 ,过点 作 ,过 边上的动点 作 ,并与 交于点 ,将 沿直线 翻折,使点 的对应点 恰好落在直线 上,求线段 的长.

一座楼梯的示意图如图所示,要在楼梯上铺一条地毯.
(1)地毯至少需多少长?(用关于a,h的代数式表示)
(2)若楼梯的宽为b,则地毯的面积为多少?
(3)当a=5m,b=1.2m,h=3m时,则地毯的面积是多少m2
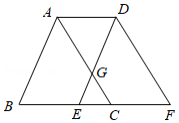
如图,将 沿 边向右平移得到 , 交 于点 .若 . .则 的值为
| A. |
2 |
B. |
4 |
C. |
6 |
D. |
8 |
在平面直角坐标系 中,将一块含有 角的直角三角板如图放置,直角顶点 的坐标为 ,顶点 的坐标为 ,顶点 恰好落在第一象限的双曲线上,现将直角三角板沿 轴正方向平移,当顶点 恰好落在该双曲线上时停止运动,则此时点 的对应点 的坐标为

A. , B. C. , D.
在一次数学研究性学习中,小兵将两个全等的直角三角形纸片 和 拼在一起,使点 与点 重合,点 与点 重合(如图 ,其中 , , ,并进行如下研究活动.
活动一:将图1中的纸片 沿 方向平移,连结 , (如图 ,当点 与点 重合时停止平移.
[思考]图2中的四边形 是平行四边形吗?请说明理由.
[发现]当纸片 平移到某一位置时,小兵发现四边形 为矩形(如图 .求 的长.
活动二:在图3中,取 的中点 ,再将纸片 绕点 顺时针方向旋转 度 ,连结 , (如图 .
[探究]当 平分 时,探究 与 的数量关系,并说明理由.

对于坐标平面内的点,现将该点向右平移1个单位,再向上平移2个单位,这种点的运动称为点 的斜平移,如点 经1次斜平移后的点的坐标为 ,已知点 的坐标为 .
(1)分别写出点 经1次,2次斜平移后得到的点的坐标.
(2)如图,点 是直线 上的一点,点 关于点 的对称点为点 ,点 关于直线 的对称点为点 .
①若 、 、 三点不在同一条直线上,判断 是否是直角三角形?请说明理由.
②若点 由点 经 次斜平移后得到,且点 的坐标为 ,求出点 的坐标及 的值.
如图1,点、点
在直线
上,反比例函数
的图象经过点
.

(1)求和
的值;
(2)将线段向右平移
个单位长度
,得到对应线段
,连接
、
.
①如图2,当时,过
作
轴于点
,交反比例函数图象于点
,求
的值;
②在线段运动过程中,连接
,若
是以
为腰的等腰三角形,求所有满足条件的
的值.
小芳和小明在手工课上各自制作楼梯模型,他们用的材料如图,则( )

| A.一样多 | B.小明多 | C.小芳多 | D.不能确定 |
如图所示,一段楼梯的高BC是3m,斜边AC是5m,如果在楼梯上铺地毯,那么至少需要地毯( )

| A.5m | B.6m | C.7m | D.8m |