如图,在矩形 中, , ,把边 沿对角线 平移,点 , 分别对应点 , 给出下列结论:
①顺次连接点 , , , 的图形是平行四边形;
②点 到它关于直线 的对称点的距离为48;
③ 的最大值为15;
④ 的最小值为 .
其中正确结论的个数是

| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
如图,在平面直角坐标系中,一次函数 的图象与 轴和 轴分别相交于 、 两点.动点 从点 出发,在线段 上以每秒3个单位长度的速度向点 作匀速运动,到达点 停止运动,点 关于点 的对称点为点 ,以线段 为边向上作正方形 .设运动时间为 秒.
(1)当 秒时,点 的坐标是 ;
(2)在运动过程中,设正方形 与 重叠部分的面积为 ,求 与 的函数表达式;
(3)若正方形 对角线的交点为 ,请直接写出在运动过程中 的最小值.

已知: 和矩形 如图①摆放(点 与点 重合),点 , , 在同一直线上, , , .如图②, 从图①的位置出发,沿 方向匀速运动,速度为 , 与 交于点 ;同时,点 从点 出发,沿 方向匀速运动,速度为 .过点 作 ,垂足为 ,交 于点 ,连接 , ,当点 停止运动时, 也停止运动.设运动时间为 ,解答下列问题:
(1)当 为何值时, ?
(2)设五边形 的面积为 ,求 与 之间的函数关系式;
(3)在运动过程中,是否存在某一时刻 ,使 ?若存在,求出 的值;若不存在,请说明理由.
(4)在运动过程中,是否存在某一时刻 ,使点 在线段 的垂直平分线上?若存在,求出 的值;若不存在,请说明理由.

如图1,抛物线 与 轴交于点 , ,与 轴交于点 ,顶点为 ,直线 交 轴于点 .
(1)求抛物线的解析式.
(2)如图2,将 沿直线 平移得到 .
①当点 落在抛物线上时,求点 的坐标.
②在 移动过程中,存在点 使 为直角三角形,请直接写出所有符合条件的点 的坐标.

如图1,经过原点 的抛物线 、 为常数, 与 轴相交于另一点 .直线 在第一象限内和此抛物线相交于点 ,与抛物线的对称轴相交于点 .

(1)求抛物线的解析式;
(2)在 轴上找一点 ,使以点 、 、 为顶点的三角形与以点 、 、 为顶点的三角形相似,求满足条件的点 的坐标;
(3)直线 沿着 轴向右平移得到直线 , 与线段 相交于点 ,与 轴下方的抛物线相交于点 ,过点 作 轴于点 .把 沿直线 折叠,当点 恰好落在抛物线上时(图 ,求直线 的解析式;
(4)在(3)问的条件下(图 ,直线 与 轴相交于点 ,把 绕点 顺时针旋转 得到△ ,点 为直线 上的动点.当△ 为等腰三角形时,求满足条件的点 的坐标.
如图①,在△ABC中, , , ,D为AB的中点,EF为△ACD的中位线,四边形EFGH为△ACD的内接矩形(矩形的四个顶点均在△ACD的边上).
(1)计算矩形EFGH的面积;
(2)将矩形EFGH沿AB向右平移,F落在BC上时停止移动.在平移过程中,当矩形与△CBD重叠部分的面积为 时,求矩形平移的距离;
(3)如图③,将(2)中矩形平移停止时所得的矩形记为矩形E1F1G1H1,将矩形E1F1G1H1绕G1点按顺时针方向旋转,当H1落在CD上时停止转动,旋转后的矩形记为矩形E2F2G1H2,设旋转角为α,求cosα的值.

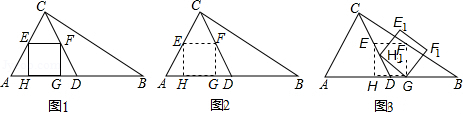
如图1,在△ ABC中,∠ ACB=90°,∠ B=30°, AC=4, D是 AB的中点, EF是△ ACD的中位线,矩形 EFGH的顶点都在△ ACD的边上.
(1)求线段 EF、 FG的长;
(2)如图2,将矩形 EFGH沿 AB向右平移,点 F落在 BC上时停止移动,设矩形移动的距离为 x,矩形与△ CBD重叠部分的面积为 S,求出 S关于 x的函数解析式;
(3)如图3,矩形 EFGH平移停止后,再绕点 G按顺时针方向旋转,当点 H落在 CD边上时停止旋转,此时矩形记作 E 1 F 1 GH 1,设旋转角为α,求cosα的值.
某校开展了一次综合实践活动,参加该活动的每个学生持有两张宽为 ,长足够的矩形纸条.探究两张纸条叠放在一起,重叠部分的形状和面积.
如图1所示,一张纸条水平放置不动,另一张纸条与它成 的角,将该纸条从右往左平移.
(1)写出在平移过程中,重叠部分可能出现的形状.
(2)当重叠部分的形状为如图2所示的四边形 时,求证:四边形 是菱形.
(3)设平移的距离为 ,两张纸条重叠部分的面积为 .求 与 的函数关系式,并求 的最大值.

如图1,抛物线 与 轴的交点 和 ,与 轴交于点 ,顶点为 .
(1)求该抛物线的解析式;
(2)连接 , , ,将 沿 轴以每秒1个单位长度的速度向左平移,得到△ ,点 、 、 的对应点分别为点 、 、 ,设平移时间为 秒,当点 与点 重合时停止移动.记△ 与四边形 重合部分的面积为 ,请直接写出 与 之间的函数关系式;
(3)如图2,过该抛物线上任意一点 向直线 作垂线,垂足为 ,试问在该抛物线的对称轴上是否存在一点 ,使得 ?若存在,请求出 的坐标;若不存在,请说明理由.
