如图1,经过原点 的抛物线 、 为常数, 与 轴相交于另一点 .直线 在第一象限内和此抛物线相交于点 ,与抛物线的对称轴相交于点 .
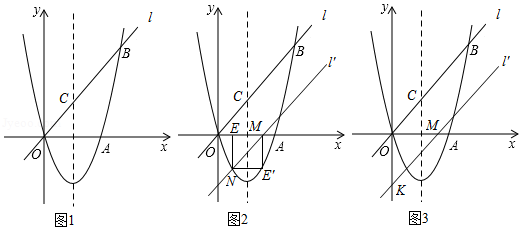
(1)求抛物线的解析式;
(2)在 轴上找一点 ,使以点 、 、 为顶点的三角形与以点 、 、 为顶点的三角形相似,求满足条件的点 的坐标;
(3)直线 沿着 轴向右平移得到直线 , 与线段 相交于点 ,与 轴下方的抛物线相交于点 ,过点 作 轴于点 .把 沿直线 折叠,当点 恰好落在抛物线上时(图 ,求直线 的解析式;
(4)在(3)问的条件下(图 ,直线 与 轴相交于点 ,把 绕点 顺时针旋转 得到△ ,点 为直线 上的动点.当△ 为等腰三角形时,求满足条件的点 的坐标.
相关知识点
推荐套卷
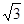 ,矩形ABOC绕点O按顺时针方向旋转60°后得矩形EFOD. 点A的对应点为点E,点B的对应点为F,点C的对应点为点D.抛物线
,矩形ABOC绕点O按顺时针方向旋转60°后得矩形EFOD. 点A的对应点为点E,点B的对应点为F,点C的对应点为点D.抛物线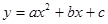 过点A、E、D.
过点A、E、D.
 ,DE⊥AB于E,交BC于F. 已知AC=6,⊙O的半径是5.
,DE⊥AB于E,交BC于F. 已知AC=6,⊙O的半径是5.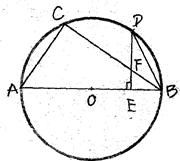

 粤公网安备 44130202000953号
粤公网安备 44130202000953号