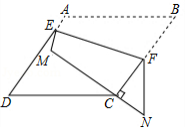
如图,在菱形中,
,点
,
分别在边
、
上,将四边形
沿
翻折,使
的对应线段
经过顶点
,当
时,
的值是 .
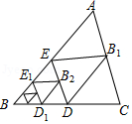
如图,将 沿着过 的中点 的直线折叠,使点 落在 边上的 处,称为第一次操作,折痕 到 的距离为 ;还原纸片后,再将 沿着过 的中点 的直线折叠,使点 落在 边上的 处,称为第二次操作,折痕 到 的距离记为 ;按上述方法不断操作下去 经过第 次操作后得到折痕 ,到 的距离记为 .若 ,则 的值为
| A. |
|
B. |
|
C. |
|
D. |
|
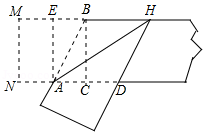
如图,正方形 在宽为2的矩形纸片一端,对折正方形 得到折痕 ,再翻折纸片,使 与 重合,以下结论错误的是
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在边长为 的菱形 中, ,过点 作 于点 ,现将 沿直线 翻折至 的位置, 与 交于点 .则 等于

| A. |
|
B. |
1 |
C. |
|
D. |
|
如图,抛物线为常数)交
轴于点
,与
轴的一个交点在2和3之间,顶点为
.
①抛物线与直线
有且只有一个交点;
②若点、点
,
、点
在该函数图象上,则
;
③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为;
④点关于直线
的对称点为
,点
、
分别在
轴和
轴上,当
时,四边形
周长的最小值为
.
其中正确判断的序号是 .

如图,把某矩形纸片沿
,
折叠(点
,
在
边上,点
,
在
边上),使点
和点
落在
边上同一点
处,
点的对称点为
点,
点的对称点为
点,若
,△
的面积为4,△
的面积为1,则矩形
的面积等于 .

如图,在 中, , , 于点 , 于点 , .连接 ,将 沿直线 翻折至 所在的平面内,得 ,连接 .过点 作 交 于点 .则四边形 的周长为

| A. |
8 |
B. |
|
C. |
|
D. |
|
如图,在 中, 是 边上的中点,连结 ,把 沿 翻折,得到 , 与 交于点 ,连结 ,若 , ,则点 到 的距离为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,把三角形纸片折叠,使点、点
都与点
重合,折痕分别为
、
,得到
,若
厘米,则
的边
的长为 厘米.

如图,正方形中,
,点
是对角线
上一点,连接
,过点
作
,交
于点
,连接
,交
于点
,将
沿
翻折,得到
,连接
,交
于点
,若点
是
边的中点,则
的周长是 .
