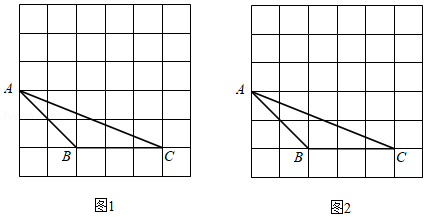
如图,在 的网格中, 的三个顶点都在格点上.
(1)在图1中画出 ,使 与 全等,顶点 在格点上.
(2)在图2中过点 画出平分 面积的直线 .
如图是由边长为1的小正方形构成的 的网格,点 , 均在格点上.
(1)在图1中画出以 为边且周长为无理数的 ,且点 和点 均在格点上(画出一个即可).
(2)在图2中画出以 为对角线的正方形 ,且点 和点 均在格点上.

如图,在 的方格纸中,线段 的端点均在格点上,请按要求画图.

(1)如图1,画出一条线段 ,使 , 在格点上;
(2)如图2,画出一条线段 ,使 , 互相平分, , 均在格点上;
(3)如图3,以 , 为顶点画出一个四边形,使其是中心对称图形,且顶点均在格点上.
如图,在 的正方形网格中,网格线的交点称为格点,点 , 在格点上,每一个小正方形的边长为1.
(1)以 为边画菱形,使菱形的其余两个顶点都在格点上(画出一个即可).
(2)计算你所画菱形的面积.

图①、图②、图③均是 的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点 、 、 均为格点.只用无刻度的直尺,分别在给定的网格中找一格点 ,按下列要求作图:
(1)在图①中,连结 、 ,使 ;
(2)在图②中,连结 、 、 ,使 ;
(3)在图③中,连结 、 ,使 .

如图,在 的方格纸 中,请按要求画格点线段(端点在格点上),且线段的端点均不与点 , , , 重合.

(1)在图1中画格点线段 , 各一条,使点 , , , 分别落在边 , , , 上,且 , 不平行 .
(2)在图2中画格点线段 , 各一条,使点 , , , 分别落在边 , , , 上,且 .
如图,在 的网格中, 的三个顶点都在格点上.
(1)在图1中画出一个以 为边的 ,使顶点 , 在格点上.
(2)在图2中画出一条恰好平分 周长的直线 (至少经过两个格点).

在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点 , ,请在所给网格区域(含边界)上按要求画整点三角形.
(1)在图1中画一个 ,使点 的横、纵坐标之和等于点 的横坐标;
(2)在图2中画一个 ,使点 , 横坐标的平方和等于它们纵坐标和的4倍.

如图,在方格纸中,点 , , 都在格点上.请按要求画出以 为边的格点四边形,使 在四边形内部(不包括边界上),且 到四边形的两个顶点的距离相等.
(1)在图甲中画出一个 .
(2)在图乙中画出一个四边形 ,使 ,且 .(注:图甲、乙在答题纸上)
(阅读理解)
用 的矩形瓷砖,可拼得一些长度不同但宽度均为 的图案.已知长度为 、 、 的所有图案如下:

(尝试操作)
如图,将小方格的边长看作 ,请在方格纸中画出长度为 的所有图案.

(归纳发现)
观察以上结果,探究图案个数与图案长度之间的关系,将下表补充完整.
图案的长度 |
|
|
|
|
|
|
所有不同图案的个数 |
1 |
2 |
3 |
|
|
|
图1是某公交公司1路车从起点站 站途经
站途经 站和
站和 站,最终到达终点站
站,最终到达终点站 站的格点站路线图.
站的格点站路线图. 的格点图是由边长为1的小正方形组成)
的格点图是由边长为1的小正方形组成)

(1)求1路车从 站到
站到 站所走的路程(精确到
站所走的路程(精确到 ;
;
(2)在图2、图3和图4的网格中各画出一种从 站到
站到 站的路线图.(要求:①与图1路线不同、路程相同;②途中必须经过两个格点站;③所画路线图不重复)
站的路线图.(要求:①与图1路线不同、路程相同;②途中必须经过两个格点站;③所画路线图不重复)
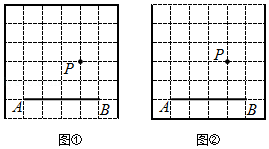
小琪同学和爸爸妈妈一起回老家给奶奶过生日,他们为奶奶准备了一个如图所示的正方形蛋糕,蛋糕的每条边上均匀镶嵌着4颗巧克力.爸爸要求小琪只切两刀把蛋糕平均分成4份,使每个人分得的蛋糕和巧克力数都相等.
(1)请你在图1中画出一种分法(无需尺规作图);
(2)如图2,小琪同学过正方形的中心切了一刀,请你用尺规作图帮她作出第2刀所在的直线.(不写作法,保留作图痕迹)

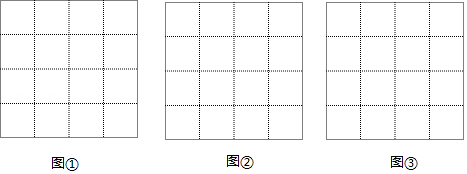
如图,在的正方形网格中,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图①中,画一个直角三角形,使它的三边长都是有理数;
(2)在图②中,画一个直角三角形,使它的一边长是有理数,另外两边长是无理数;
(3)在图③中,画一个直角三角形,使它的三边长都是无理数.
如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点.四边形的顶点在格点上,点
是边
与网格线的交点.请选择适当的格点,用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由.
(1)如图1,过点画线段
,使
,且
.
(2)如图1,在边上画一点
,使
.
(3)如图2,过点画线段
,使
,且
.
