初中数学三角形的内切圆与内心解答题

已知任意三角形的三边长，如何求三角形面积？

古希腊的几何学家海伦解决了这个问题，在他的著作《度量论》一书中给出了计算公式﹣﹣海伦公式 $S=\sqrt{p(p-a)(p-b)(p-c)}$（其中a，b，c是三角形的三边长， $p=\frac{a+b+c}{2}$，S为三角形的面积），并给出了证明

例如：在△ABC中，a＝3，b＝4，c＝5，那么它的面积可以这样计算：

∵a＝3，b＝4，c＝5

∴ $p=\frac{a+b+c}{2}=6$

∴ $S=\sqrt{p(p-a)(p-b)(p-c)}=\sqrt{6\times 3\times 2\times 1}=6$

事实上，对于已知三角形的三边长求三角形面积的问题，还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决．

根据上述材料，解答下列问题：

如图，在△ABC中，BC＝5，AC＝6，AB＝9

（1）用海伦公式求△ABC的面积；

（2）求△ABC的内切圆半径r．

（1）如图，已知线段和点，利用直尺和圆规作，使点是的内心（不写作法，保留作图痕迹）；

（2）在所画的中，若，，，则的内切圆半径是　　．

如图，点是的内心，的延长线与的外接圆交于点，与交于点，延长、相交于点，的平分线交于点．

（1）求证：；

（2）求证：；

（3）若，，求的长．

如图，点是的内心，的延长线和的外接圆相交于点，过作直线．

（1）求证：是的切线；

（2）若，，求优弧的长．

如图， $\mathit{PA}$ 是 $\odot O$ 的切线，切点为 $A$ ， $\mathit{AC}$ 是 $\odot O$ 的直径，连接 $\mathit{OP}$ 交 $\odot O$ 于 $E$ ．过 $A$ 点作 $\mathit{AB}\perp \mathit{PO}$ 于点 $D$ ，交 $\odot O$ 于 $B$ ，连接 $\mathit{BC}$ ， $\mathit{PB}$ ．

（1）求证： $\mathit{PB}$ 是 $\odot O$ 的切线；

（2）求证： $E$ 为 $\mathit{\Delta PAB}$ 的内心；

（3）若 $\cos \angle \mathit{PAB}=\frac{\sqrt{10}}{10}$ ， $\mathit{BC}=1$ ，求 $\mathit{PO}$ 的长．

如图，顶点为的抛物线与轴交于，两点，与轴交于点．

（1）求这条抛物线对应的函数表达式；

（2）问在轴上是否存在一点，使得为直角三角形？若存在，求出点的坐标；若不存在，说明理由．

（3）若在第一象限的抛物线下方有一动点，满足，过作轴于点，设的内心为，试求的最小值．

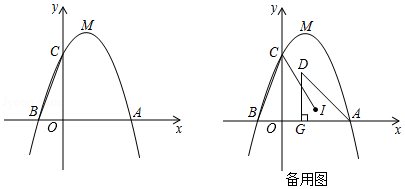
如图，，点、分别在射线、上，，．

（1）用尺规在图中作一段劣弧，使得它在、两点分别与射线和相切．要求：写出作法，并保留作图痕迹；

（2）根据（1）的作法，结合已有条件，请写出已知和求证，并证明；

（3）求所得的劣弧与线段、围成的封闭图形的面积．

已知关于的一元二次方程．

（1）求证：无论为任何实数，此方程总有两个实数根；

（2）若方程的两个实数根为、，满足，求的值；

（3）若的斜边为5，另外两条边的长恰好是方程的两个根、，求的内切圆半径．

阅读以下材料，并按要求完成相应的任务：

莱昂哈德欧拉是瑞士数学家，在数学上经常见到以他的名字命名的重要常数，公式和定理，下面就是欧拉发现的一个定理：在中，和分别为外接圆和内切圆的半径，和分别为其中外心和内心，则．

如图1，和分别是的外接圆和内切圆，与相切分于点，设的半径为，的半径为，外心（三角形三边垂直平分线的交点）与内心（三角形三条角平分线的交点）之间的距离，则有．

下面是该定理的证明过程（部分）

延长交于点，过点作的直径，连接，．

，（同弧所对的圆周角相等）．

．，，①

如图2，在图1（隐去，的基础上作的直径，连接，，，．

是的直径，所以．

与相切于点，所以，

．

（同弧所对的圆周角相等），

，

．

②

任务：（1）观察发现：，　　（用含，的代数式表示）；

（2）请判断和的数量关系，并说明理由．

（3）请观察式子①和式子②，并利用任务（1），（2）的结论，按照上面的证明思路，完成该定理证明的剩余部分；

（4）应用：若的外接圆的半径为，内切圆的半径为，则的外心与内心之间的距离为　　．

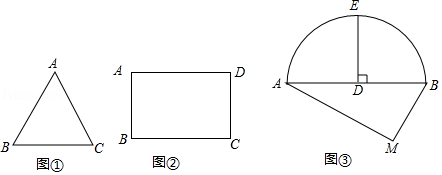
问题提出

（1）如图①，是等边三角形，，若点是的内心，则的长为　　；

问题探究

（2）如图②，在矩形中，，，如果点是边上一点，且，那么边上是否存在一点，使得线段将矩形的面积平分？若存在，求出的长；若不存在，请说明理由．

问题解决

（3）某城市街角有一草坪，草坪是由草地和弦与其所对的劣弧围成的草地组成，如图③所示．管理员王师傅在处的水管上安装了一喷灌龙头，以后，他想只用喷灌龙头来给这块草坪浇水，并且在用喷灌龙头浇水时，既要能确保草坪的每个角落都能浇上水，又能节约用水，于是，他让喷灌龙头的转角正好等于（即每次喷灌时喷灌龙头由转到，然后再转回，这样往复喷灌．同时，再合理设计好喷灌龙头喷水的射程就可以了．

如图③，已测出，，的面积为；过弦的中点作交于点，又测得．

请你根据以上信息，帮助王师傅计算喷灌龙头的射程至少多少米时，才能实现他的想法？为什么？（结果保留根号或精确到0.01米）

如图，，为中点，点在线段上（不与点，重合），将绕点逆时针旋转后得到扇形，，分别切优弧于点，，且点，在异侧，连接．

（1）求证：；

（2）当时，求的长（结果保留；

（3）若的外心在扇形的内部，求的取值范围．