如图,直线与
相离,
于点
,与
相交于点
,
.
是直线
上一点,连结
并延长交
于另一点
,且
.
(1)求证:是
的切线;
(2)若的半径为3,求线段
的长.

如图,是
的直径,点
是
延长线上一点,过点
作
的切线
,切点是
,过点
作弦
于
,连接
,
.
(1)求证:是
的切线;
(2)若,
,求
的长;
(3)试探究线段,
,
之间的数量关系,并说明理由.

如图,是
的直径,点
为
上一点,
于点
,交
于点
,点
为
的延长线上一点,
的延长线与
的延长线交于点
,且
,连结
、
、
.
(1)求证:为
的切线;
(2)过作
于点
,求证:
;
(3)如果,
,求
的长.

已知在平面直角坐标系中,直线
分别交
轴和
轴于点
,
.
(1)如图1,已知经过点
,且与直线
相切于点
,求
的直径长;
(2)如图2,已知直线分别交
轴和
轴于点
和点
,点
是直线
上的一个动点,以
为圆心,
为半径画圆.
①当点与点
重合时,求证:直线
与
相切;
②设与直线
相交于
,
两点,连结
,
.问:是否存在这样的点
,使得
是等腰直角三角形,若存在,求出点
的坐标;若不存在,请说明理由.

如图,为
的直径,点
为
上一点,将弧
沿直线
翻折,使弧
的中点
恰好与圆心
重合,连接
,
,
,过点
的切线与线段
的延长线交于点
,连接
,在
的另一侧作
.
(1)判断与
的位置关系,并说明理由;
(2)若,求四边形
的面积.
如图,在中.
,以
为直径的
分别交
、
于点
、
,点
在
的延长线上,且
.
(1)求证:是
的切线;
(2)若,
,求点
到
的距离.

如图,在中,
,点
在
上,以
为半径作
,与
相交于点
,与
相切于点
,过点
作
,垂足为
.
(1)求证:是
的切线;
(2)若,
,求
的半径.

如图,在中,
,
是
的外接圆,点
在
上,且
,过点
作
的垂线,与
的延长线相交于点
,并与
的延长线相交于点
.
(1)求证:是
的切线;
(2)若的半径
,
,求
的长.

如图1,为半圆的直径,点
为圆心,
为半圆的切线,过半圆上的点
作
交
于点
,连接
.
(1)连接,若
,求证:
是半圆的切线;
(2)如图2,当线段与半圆交于点
时,连接
,
,判断
和
的数量关系,并证明你的结论.

如图,在中,
,点
为
的中点,延长
到点
,使
,
交
于点
.
(1)求证:是
的切线;
(2)若,求弦
的长.

在平面内,给定不在同一条直线上的点,
,
,如图所示,点
到点
,
,
的距离均等于
为常数),到点
的距离等于
的所有点组成图形
,
的平分线交图形
于点
,连接
,
.
(1)求证:;
(2)过点作
,垂足为
,作
,垂足为
,延长
交图形
于点
,连接
.若
,求直线
与图形
的公共点个数.
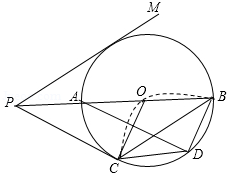
(年贵州省黔东南州)如图,已知PC平分∠MPN,点O是PC上任意一点,PM与⊙O相切于点E,交PC于A、B两点.
(1)求证:PN与⊙O相切;
(2)如果∠MPC=30°,PE= ,求劣弧
,求劣弧 的长.
的长.
(年贵州省黔南州)如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD=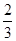 .
.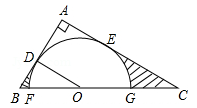
(1)求⊙O的半径OD;
(2)求证:AE是⊙O的切线;
(3)求图中两部分阴影面积的和.
(黔西南州)如图所示,点O在∠APB的平分线上,⊙O与PA相切于点C.
(1)求证:直线PB与⊙O相切
(2)PO的延长线与⊙O交于点E,若⊙O的半径为3,PC=4.求弦CE的长.