初中数学圆内接四边形的性质试题

如图1，已知：抛物线y=x²+bx+c与x轴交于A，B两点，与y轴交于点C，经过B，C两点的直线是y=x-2，连结AC．

（1）求出抛物线的函数关系式；
（2）若△ABC内部能否截出面积最大的矩形DEFC（顶点D、E、F、G在△ABC各边上）？若能，求出在AB边上的矩形顶点的坐标；若不能，请说明理由．
（3）点P（t，0）是x轴上一动点，P、Q两点关于直线BC成轴对称，PQ交BC于点M，作QH⊥x轴于点H．连结OQ，是否存在t的值，使△OQH与△APM相似？若存在，求出t的值；若不存在，说明理由．

如图，设四边形ABCD是边长为1的正方形，以对角线AC为边作第二个正方形ACEF、再以对角线AE为边作笫三个正方形AEGH，如此下去…．若正方形ABCD的边长记为a₁，按上述方法所作的正方形的边长依次为a₂，a₃，a₄，…，a_n，则a_n=          ．

如图，A、B、C、D为矩形的4个顶点，AB=16cm，BC=6cm，动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发，点Q从点C向点D移动．

（1）若点P从点A移动到点B停止，点P、Q分别从点A、C同时出发，问经过2s时P、Q两点之间的距离是多少cm？
（2）若点P从点A移动到点B停止，点Q随点P的停止而停止移动，点P、Q分别从点A、C同时出发，问经过多长时间P、Q两点之间的距离是10cm？
（3）若点P沿着AB→BC→CD移动，点P、Q分别从点A、C同时出发，点Q从点C移动到点D停止时，点P随点Q的停止而停止移动，试探求经过多长时间△PBQ的面积为12cm²？

已知抛物线y=x²+1（如图所示）．

（1）填空：抛物线的顶点坐标是（     ，        ），对称轴是            ；
（2）已知y轴上一点A（0，2），点P在抛物线上，过点P作PB⊥x轴，垂足为B．若△PAB是等边三角形，求点P的坐标；
（3）在（2）的条件下，点M在直线AP上．在平面内是否存在点N，使四边形OAMN为菱形？若存在，直接写出所有满足条件的点N的坐标；若不存在，请说明理由．

在如图中，每个正方形有边长为1 的小正方形组成：

（1）观察图形，请填写下列表格：

正方形边长	1	3	5	7	…	n（奇数）
黑色小正方形个数					…
正方形边长	2	4	6	8	…	n（偶数）
黑色小正方形个数					…

（2）在边长为n（n≥1）的正方形中，设黑色小正方形的个数为P₁，白色小正方形的个数为P₂，问是否存在偶数n，使P₂＝5P₁？若存在，请写出n的值；若不存在，请说明理由.

如图1，点E为正方形ABCD的边AB上一点，EF⊥EC，且EF=EC，连接AF．

（1）求∠EAF的度数；
（2）如图2，连接FC交BD于M，交AD于N．
①求证：AD=AF+2DM；
②若AF=10，AN=12，则MD的长为  ．

如图1，四边形ABCD是正方形，点G是BC边上任意一点，DE⊥AG于点E，BF∥DE且交AG于点F．

（1）求证：AE=BF；
（2）如图2，连接DF、CE，探究线段DF与CE的关系并证明；
（3）图1中，若AB=4，BG=3，求EF长．

如图，在正方形ABCD中，点E是BC的中点，将△ABE沿AE折叠后得到△AFE，点F在正方形ABCD的内部，延长AF交CD于点G．

（1）猜想并证明线段GF与GC的数量关系；
（2）若将图1中的正方形改成矩形，其它条件不变，如图2，那么线段GF与GC之间的数量关系是否改变？请证明你的结论；
（3）若将图1中的正方形改成平行四边形，其它条件不变，如图3，那么线段GF与GC之间的数量关系是否会改变？请证明你的结论．

如图，正方形ABCD中，点E，F分别在AD，DC上，且△BEF为等边三角形，下列结论：
①DE=DF；②∠AEB=75°；③BE=DE；④AE+FC=EF．
其中正确的结论个数有（    ）

A．1个

B．2个

C．3个

D．4个

如图，ABCD是正方形场地，点E在DC的延长线上，AE与BC相交于点F．有甲、乙、丙三名同学同时从点A出发，甲沿着A﹣B﹣F﹣C的路径行走至C，乙沿着A﹣F﹣E﹣C﹣D的路径行走至D，丙沿着A﹣F﹣C﹣D的路径行走至D．若三名同学行走的速度都相同，则他们到达各自的目的地的先后顺序（由先至后）是（   ）

A．甲乙丙 B．甲丙乙 C．乙丙甲 D．丙甲乙

如图（1），在矩形ABCD中，AB=6，BC=2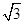，点O是AB的中点，点P在AB的延长线上，且BP=3．一动点E从O点出发，以每秒1个单位长度的速度沿OA匀速运动，到达A点后，立即以原速度沿AO返回；另一动点F从P点出发，以每秒1个单位长度的速度沿射线PA匀速运动，点E、F同时出发，当两点相遇时停止运动，在点E、F的运动过程中，如图（2）以EF为边作等边△EFG，使△EFG和矩形ABCD在射线PA的同侧．设运动的时间为t秒（t＞0）．

（1）如图（3），当等边△EFG的边FG恰好经过点C时，求运动时间t的值；
（2）如图（4），当等边△EFG的顶点G恰好落在CD边上时，求运动时间t的值；
（3）在整个运动过程中，设等边△EFG和矩形ABCD重叠部分的面积为S，请求出S与t之间的函数关系式，并写出相应的自变量的取值范围．

数学活动课上，老师给出如下问题：如图，将等腰直角三角形纸片沿斜边上的高AC剪开，得到等腰直角三角形△ABC与△EFD，将△EFD的直角顶点在直线BC上平移，在平移的过程中，直线AC与直线DE交于点Q，让同学们探究线段BQ与AD的数量关系和位置关系．
请你阅读下面交流信息，解决所提出的问题．
展示交流：
小敏：满足条件的图形如图甲所示图形，延长BQ与AD交于点H．我们可以证明△BCQ≌△ACD，从而易得BQ=AD，BQ⊥AD．
小慧：根据图甲，当点F在线段BC上时，我们可以验证小慧的说法是正确的．但当点F在线段CB的延长线上（如图乙）或线段CB的反向延长线上（如图丙）时，我对小慧说法的正确性表示怀疑．
（1）请你帮助小慧进行分析，小敏的结论在图乙、图丙中是否成立？请说明理由．
（选择图乙或图丙的一种情况说明即可）．

（2）小慧思考问题的方式中，蕴含的数学思想是            ．
拓展延伸：
根据你上面选择的图形，分别取AB、BD、DQ、AQ的中点M、N、P、T．则四边形MNPT是什么样的特殊四边形？请说明理由．

一块矩形塑料板ABCD，AD=10，AB=4．将一块足够大的直角三角板PHF的直角顶点P置于AD边上（不于A、D 重合，任意移动P点和三角板PHF的位置，如图（1）．

（1）△PEF是否存在这样的位置，使两边直角边分别通过B、C两点？如图（2），若存在，请求出AP的长度，若不存在，请说理由．
（2）PH始终通过B点时，PF交BC于E点，交DC的延长线于Q点，△PHF是否存在这样的位置，使得CE=2？若能请求出这时AP的长度；若不能，请说明理由．

如图，在直角坐标系中，四边形OABC的OA，OC两边分别在x，y轴上，OA∥BC，BC=15cm，A点坐标为（16，0），C点坐标为（0，4）．点P，Q分别从C，A同时出发，点P以2cm/s的速度由C向B运动，点Q以4cm/s的速度由A向O运动，当点Q到达点O时，点P也停止运动，设运动时间为t秒（0≤t≤4）．

（1）求当t为多少时，四边形PQAB为平行四边形？
（2）求当t为多少时？PQ所在直线将四边形OABC分成左右两部分的面积比为1：2；
（3）直接写出在（2）的情况下，直线PQ的函数关系式．

如图，周长为16的菱形ABCD中，点E，F分别在AB，AD边上，AE=1，AF=3，P为BD上一动点，则线段EP+FP的长最短为（   ）

A．3

B．4

C．5

D．6