已知抛物线y=
x2+1（如图所示）．
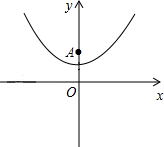
（1）填空：抛物线的顶点坐标是（ ， ），对称轴是 ；
（2）已知y轴上一点A（0，2），点P在抛物线上，过点P作PB⊥x轴，垂足为B．若△PAB是等边三角形，求点P的坐标；
（3）在（2）的条件下，点M在直线AP上．在平面内是否存在点N，使四边形OAMN为菱形？若存在，直接写出所有满足条件的点N的坐标；若不存在，请说明理由．
a），其中a=－2。
(2)1－
=
.
.
.
，CD=
，AC=
，BC=
，试说明：
>
.相关知识点
推荐套卷
已知抛物线y=x2+1（如图所示）．
（1）填空：抛物线的顶点坐标是（ ， ），对称轴是 ；
（2）已知y轴上一点A（0，2），点P在抛物线上，过点P作PB⊥x轴，垂足为B．若△PAB是等边三角形，求点P的坐标；
（3）在（2）的条件下，点M在直线AP上．在平面内是否存在点N，使四边形OAMN为菱形？若存在，直接写出所有满足条件的点N的坐标；若不存在，请说明理由．
粤公网安备 44130202000953号