山西省吕梁市孝义市中考一模数学试卷
如图,直线a∥b,AB⊥BC,∠1=40°,则∠2的度数为( )

| A.30° | B.40° | C.50° | D.60° |
2014年,我国经济社会发展总体平稳,稳中有进,国内生产总值比上年增长7.4%,达到636000亿元,这一数据用科学记数法表示为( )
A.0.636× 元 元 |
B.0.636× 元 元 |
C.6.36× 元 元 |
D.6.36× 元 元 |
一次函数y=(m+2)x+(1+m)的图象如图所示,则m的取值范围是( )

| A.m>﹣1 | B.m<﹣2 | C.﹣2<m<﹣1 | D.m<﹣1 |
下列说法中不正确的是( )
| A.抛掷一枚硬币,硬币落地时正面朝上是随机事件 |
| B.把4个球放入三个抽屉中,其中一个抽屉中至少有2个球是必然事件 |
| C.任意打开七年级下册数学教科书,正好是97页是随机事件 |
| D.某种彩票的中奖率为0.001,则买100张彩票一定有1张中奖 |
一元二次方程 ﹣6x+8=0的根的情况是( )
﹣6x+8=0的根的情况是( )
| A.有两个不相等的实数根 | B.有两个相等的实数根 |
| C.有一个实数根 | D.没有实数根 |
如图,AB为⊙O的直径,C为⊙O外一点,过点C作⊙O的切线,切点为B,连接AC交⊙O于点D,∠C=40°,点E在AB左侧的半圆上运动(不与A、B重合),则∠AED的大小是( )

A.20° B.40° C.50° D.80°
如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=5,AC=6,则tan∠DCB的值是( )

A. |
B. |
C. |
D. |
甲、乙两种水稻品种经过连续5年试验种植,每年的单位面积产量的折线图如图所示,经过计算,甲的单位面积平均产量 甲=10,乙的单位面积平均产量
甲=10,乙的单位面积平均产量 乙=10,则根据图表估计,两种水稻品种产量比较稳定的是 .
乙=10,则根据图表估计,两种水稻品种产量比较稳定的是 .

如图,某公园的一角有一块草坪(阴影部分),实线部分是沿草坪外围的一条小路,小路由两条相等的线段AC、BD和圆弧CD组成,其中AC、BD分别与圆弧CD相切于点C、D.经过测量,线段CD与半径OD都为60米,则这条小路的长度为 米.
如图,四边形ABCD为矩形,AB=6,BC=8,E为AB的中点,将矩形ABCD折叠,使得点D与点E重合,折痕为MN,则折痕MN的长度为 .

在如图所示的平面直角坐标系中,每个小正方形的边长均为1,△ABC的顶点都在格点上.
实践操作:
(1)在格点图中,将△ABC以原点O为旋转中心,顺时针旋转90°,画出旋转后的△A1B1C1;
(2)画出△A1B1C1关于x轴对称的△A2B2C2;
学习反思:
△ABC与△A2B2C2是否关于某直线对称?若对称,请直接写出对称轴所在直线的解析式;若不对称,请说明理由.
某校为了了解学生的体能状况,决定抽取部分同学进行体育测试参加测试的每名学生从“1000米跑步”、“立定跳远”,“1分钟跳绳”、“坐位体前屈”四个项目中随机抽取两项作为测试项目.
(1)求:小明同学恰好抽到“立定跳远”,“坐位体前屈”两项的概率.
(2)据统计,初二三班共10名学生参加了测试,两项的平均成绩如下:
94 100 90 84 92 50 89 64 71 92
①该表是这10名同学平均成绩的一些统计数据,请将表格中缺少的数据补充完整.
平均数 中位数 众数
82.6
②为了调动学生参与体育锻炼的积极性,该班决定对参与测试的同学进行奖励,决定制定一个奖励标准,成绩凡达到或超过这个标准的学生将受到奖励,如果要使参与测试的学生半数左右能获奖,根据上面的计算结果,这个标准应定为多少?并简述理由.
某中学综合实践小组同学,想测量金龙山观音大佛的高度,他们在山脚下的D处测得山顶B的仰角为30°,沿着山脚向前走了4米达到E处,测得观音大佛的头顶A的倾角为45°,已知金龙山的山顶距地面的标高(线段BC的长度)为60米,请计算观音大佛的高度为多少米?(结果精确到0.1米, ≈1.73)
≈1.73)
某体育用品公司以每件60元的批发价购回一批“电子智能跳绳”,第一周以每件120元的价格进行销售,第二周以每件110元的价格进行销售,结果两周共销售该款跳绳100件,两周共实现销售额11400元.
(1)求该公司第一周和第二周分别销售了电子智能跳绳多少件?
(2)为了追求利润的最大化,该公司决定第三周在第二周的基础上降价销售,公司营销部经过分析发现,如果第三周的销售价在第二周的基础上每降价1元,销售量则会在第二周的基础上增加2件,求第三周的销售价定为多少时,该周的销售利润最大?最大利润为多少元?
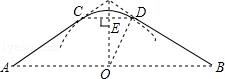
数学活动课上,老师给出如下问题:如图,将等腰直角三角形纸片沿斜边上的高AC剪开,得到等腰直角三角形△ABC与△EFD,将△EFD的直角顶点在直线BC上平移,在平移的过程中,直线AC与直线DE交于点Q,让同学们探究线段BQ与AD的数量关系和位置关系.
请你阅读下面交流信息,解决所提出的问题.
展示交流:
小敏:满足条件的图形如图甲所示图形,延长BQ与AD交于点H.我们可以证明△BCQ≌△ACD,从而易得BQ=AD,BQ⊥AD.
小慧:根据图甲,当点F在线段BC上时,我们可以验证小慧的说法是正确的.但当点F在线段CB的延长线上(如图乙)或线段CB的反向延长线上(如图丙)时,我对小慧说法的正确性表示怀疑.
(1)请你帮助小慧进行分析,小敏的结论在图乙、图丙中是否成立?请说明理由.
(选择图乙或图丙的一种情况说明即可).

(2)小慧思考问题的方式中,蕴含的数学思想是 .
拓展延伸:
根据你上面选择的图形,分别取AB、BD、DQ、AQ的中点M、N、P、T.则四边形MNPT是什么样的特殊四边形?请说明理由.

 ,0,1中,最小的实数是( )
,0,1中,最小的实数是( )





 =16
=16
 =
= ﹣4a
﹣4a = .
= . ),B(﹣1,
),B(﹣1, ),C(2,
),C(2, )都在反比例函数y=
)都在反比例函数y= 的图象上,那么
的图象上,那么 、5
、5 、7
、7 、9
、9 、11
、11 …它们是按一定规律排列的,那么这列式子的第n个单项式是 .
…它们是按一定规律排列的,那么这列式子的第n个单项式是 . +sin60°+
+sin60°+
 ﹣a(a﹣b),其中a=1,b=﹣2.
﹣a(a﹣b),其中a=1,b=﹣2. .
. +3与x轴分别交于A、B两点(A在B的左侧),与y轴交于点C.
+3与x轴分别交于A、B两点(A在B的左侧),与y轴交于点C.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号