如图1,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F.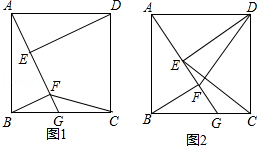
(1)求证:AE=BF;
(2)如图2,连接DF、CE,探究线段DF与CE的关系并证明;
(3)图1中,若AB=4,BG=3,求EF长.
相关知识点
推荐套卷
如图1,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F.
(1)求证:AE=BF;
(2)如图2,连接DF、CE,探究线段DF与CE的关系并证明;
(3)图1中,若AB=4,BG=3,求EF长.