已知在长方形ABCD中，AB＝4，BC＝
，O为BC上一点，BO＝
，如图所示，以BC所在直线为x轴，O为坐标原点建立平面直角坐标系，M为线段OC上的一点．
（1）若点M的坐标为（1，0），如图①，以OM为一边作等腰△OMP，使点P在长方形ABCD的一边上，则符合条件的等腰三角形有几个？请直接写出所有符合条件的点P的坐标；
（2）若将（1）中的点M的坐标改为（4，0），其它条件不变，如图②，那么符合条件的等腰三角形有几个？求出所有符合条件的点P的坐标；
（3）若将（1）中的点M的坐标改为（5，0），其它条件不变，如图③，请直接写出符合条件的等腰三角形有几个？请直接写出所有符合条件的点P的坐标．
如图，长方形ABCO的顶点A、C、O都在坐标轴上，点B的坐标为（8，3），M为AB的中点．
（1）试求点M的坐标和△AOM的周长；
（2）若P是OC上的一个动点，它以每秒1个单位长度的速度从点C出发沿射线CO方向匀速运动，设运动时间为t秒（t＞0）．
①若△POM的面积等于△AOM的面积的一半，试求t的值；
②是否存在某一时刻t，使△POM是等腰三角形？若存在，求出此时t的值；若不存在，试说明理由．
如图，把长方形纸片ABCD沿EF折叠后，使得点D与点B重合，点C落在点C′的位置上．
（1）△BEF是等腰三角形吗？试说明理由；
（2）若AB＝8，DE＝10，求CF的长度．
如图，在平行四边形ABCD中，E、F分别为边AB、CD的中点，连接DE、BF．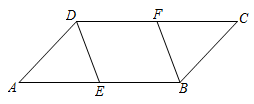
求证：△ADE≌△CBF．
四边形ABCD是正方形，E、F分别是DC和CB的延长线上的点，且DE=BF，连接AE、AF、EF．
（1）试判断△AEF的形状，并说明理由；
（2）填空：△ABF可以由△ADE绕旋转中心 点，按顺时针方向旋转 度得到；
（3）若BC=8，则四边形AECF的面积为 ．（直接写结果）
在矩形ABCD中，AB=6cm，BC=12cm，点P从点A 出发沿AB以1cm/s的速度向点B移动；同时，点Q从点B出发以2cm/s的速度向点C移动．
（1）写出△DPQ的面积s与时间t的函数关系式．
（2）几秒钟后△DPQ的面积等于28cm2．
如图，O是正六边形ABCDEF的中心，连接BD、DF、FB，
（1）设△BDF的面积为S1，正六边形ABCDEF的面积为S2 ，则S1与S2的数量关系是 ；
（2）△ABF通过旋转可与△CDB重合，请指出旋转中心和最小旋转角的度数．
如图，在△ABC中，AD平分∠BAC，按如下步骤作图：
第一步，分别以点A、D为圆心，以大于
AD的长为半径在AD两侧作弧，交于两点M、N；
第二步，连接MN分别交AB、AC于点E、F；
第三步，连接DE、DF．
（1）求证：四边形AEDF是菱形；
（2）若BD=6，AF=4，CD=3，求BE的长．
如图，在△ABC中，AB=AC，D为边BC上一点，以AB，BD为邻边作▱ABDE，连接AD，EC．
（1）求证：△ADC≌△ECD；
（2）若BD=CD，求证：四边形ADCE是矩形
如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF=BD，连接BF．
（1）线段BD与CD有什么数量关系，并说明理由；
（2）当△ABC满足什么条件时，四边形AFBD是矩形？并说明理由．
如图，菱形ABCD的周长为40cm，它的一条对角线BD长10cm．
（1）求菱形的每一个内角的度数．
（2）求菱形另一条对角线AC的长．
如图，△ABC中，∠A=80°，BE，CF交于点O，∠ACF＝30°，∠ABE＝20°，求∠BOC的度数．
一个多边形的内角和是它的外角和的5倍，求这个多边形的边数．
如图，矩形ABCD中，AB=8，BC=6，P为AD上一点，将△ABP沿BP翻折至△EBP，PE与CD相交于点O，且OE=OD．
（1）求证：OP=OF；
（2）求AP的长．
粤公网安备 44130202000953号