如图，等腰直角△ABC（∠C＝90°）的直角边长与正方形MNPQ的边长均为6cm，CA与MN在同一直线上，开始时A点与M点重合，让△ABC向右平移，直到C点与M点重合时为止，设△ABC与正方形MNPQ的重叠部分（图中阴影部分）的面积为ycm2，MA的长度为xcm．
（1）试写出y与x之间的函数表达式；
（2）当MA＝4㎝时，重叠部分的面积是多少？
（3）当MA的长度是多少时，等腰直角△ABC与正方形MNPQ的重叠部分以外的四边形BCMD的面积与重叠部分的面积比为3：1？
（4）开始时等腰直角△ABC中A点与M点重合，已知△ABC向右移动的速度是1cm/s，在A点与N点重合后继续向右移动，当运动停止时边BC与PN重合，探究重叠部分的面积y（cm2）与运动时间t（s）的函数表达式．
一张长方形纸片，剪下一个正方形，剩下一个长方形，称为第一次操作；在剩下的长方形纸片中再剪下一个正方形，剩下一个长方形，称为第二次操作；…；若在第
次操作后，剩下的长方形为正方形，则称原长方形为阶奇异长方形．如图1，长方形ABCD中，若AB＝2，BC＝6，则称长方形ABCD为2阶奇异长方形．
（1）判断与操作：如图2，长方形ABCD长为10，宽为4，它是奇异长方形，请写出它是____阶奇异长方形，并在图中画出裁剪线；
（2）探究与计算：已知长方形ABCD的一边长为30，另一边长为a（a<30），且它是3阶奇异长方形，请画出所有可能的长方形ABCD及裁剪线的示意图，并求出相应的
值．
如图，将长方形纸片ABCD沿对角线BD折叠得到△BDE，DE交AB于点G．
（1）求证：DG＝BG；
（2）若AD＝4，AB＝8，求△BDG的面积．
对于边长为3的正方形ABCD，建立适当的直角坐标系，写出各个顶点的坐标．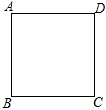
如图1，在直角坐标系中，点A的坐标为（1，0），以OA为一边在第一象限内作正方形OABC，点D是x轴正半轴上一动点（OD>1，且OD≠2），连接BD，以BD为边在第一象限内作正方形DBFE，设M为正方形DBFE的中心，直线MA交y轴于点N．如果定义：只有一组对角是直角的四边形叫做损矩形．
（1）试找出图1中的一个损矩形 ；
（2）试说明（1）中找出的损矩形一定有外接圆；
（3）随着点D的位置变化，点N的位置是否会发生变化？若没有发生变化，求出点N的坐标；若发生变化，请说明理由．
（4）在图2中，过点M作MG⊥y轴，垂足是点G，连结DN，若四边形DMGN为损矩形，求点D的坐标．
在一个边长为a（单位：cm）的正方形ABCD中，点E、M分别是线段AC，CD上的动点，连结DE并延长交正方形的边于点F，过点M作MN⊥DF于H，交AD于N．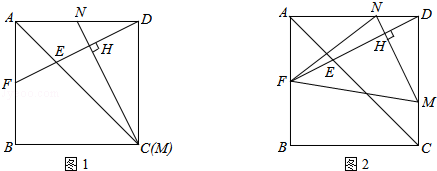
（1）如图1，当点M与点C重合，求证：DF=MN；
（2）如图2，假设点M从点C出发，以1cm/s的速度沿CD向点D运动，点E同时从点A出发，以
cm/s速度沿AC向点C运动，运动时间为t（t＞0）；
①判断命题“当点F是边AB中点时，则点M是边CD的三等分点”的真假，并说明理由．
②连结FM、FN，△MNF能否为等腰三角形？若能，请写出a，t之间的关系；若不能，请说明理由．
如图，点P是菱形ABCD对角线AC上的一点，连接DP并延长DP交边AB于点E，连接BP并延长交边AD于点F，交CD的延长线于点G．
（1）求证：△APB≌△APD；
（2）已知DF：FA=1：2，设线段DP的长为x，线段PF的长为y．
①求y与x的函数关系式；
②当x=6时，求线段FG的长．
如图，矩形ABCD中，E为BC上一点，DF⊥AE于F．
（1）ΔABE与ΔADF相似吗？请说明理由．
（2）若AB=6，AD=12，BE=8，求FD的长．
如图，△BAD是由△BEC在平面内绕点B旋转60°而得，且AB⊥BC，BE=CE，连接DE．
（1）求证：△BDE≌△BCE；
（2）试判断四边形ABED的形状，并说明理由．
如图，矩形OABC是一张放在平面直角坐标系中的矩形纸片，点A在x轴上，点C在y轴上，OA=10、OC=8，
（1）如图，在AB上取一点E，使得△CBE沿CE翻折后，点B落在x轴上，记作点D．求点D的坐标；
（2）求折痕CE所在直线的解析式．
如图，在▱ABCD中，∠ABD的平分线BE交AD于点E，∠CDB的平分线DF交BC于点F，连接BD．
（1）求证：△ABE≌△CDF；
（2）若AB=DB，求证：四边形DFBE是矩形．
，问这个多边形共有多少条对角线？
粤公网安备 44130202000953号