陕西省西安市莲湖区五校联考九年级上学期期中数学试卷
一元二次方程x2-2x=0的根是( )
| A.x1=0,x2=-2 | B.x1=1,x2=2 | C.x1=1,x2=-2 | D.x1=0,x2=2 |
下列事件中,是必然事件的是( )
| A.打开电视机,正在播放新闻 |
| B.父亲年龄比儿子年龄大 |
| C.通过长期努力学习,你会成为数学家 |
| D.下雨天,每个人都打着雨伞 |
如图,矩形的两条对角线的一个交角为60°,两条对角线的长度的和为20cm,则这个矩形的一条较短边的长度为( )
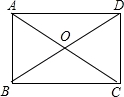
| A.10cm | B.8cm | C.6cm | D.5cm |
下列命题正确的是( )
| A.一组对边相等,另一组对边平行的四边形一定是平行四边形 |
| B.对角线相等的四边形一定是矩形 |
| C.两条对角线互相垂直的四边形一定是菱形 |
| D.两条对角线相等且互相垂直平分的四边形一定是正方形 |
如图,下列条件不能判定△ABC与△ADE相似的是( )

A. |
B.∠B=∠ADE |
C. |
D.∠C=∠AED |
若关于x的一元二次方程(k-1)x2+2x-2=0有不相等实数根,则k的取值范围是( )
A.k> |
B.k≥ |
C.k> 且k≠1 且k≠1 |
D.k≥ 且k≠1 且k≠1 |
如图,身高为1.5米的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3米,CA=1米,则树的高度为( )

| A.4.5米 | B.6米 | C.3米 | D.4米 |
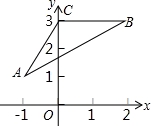
某校幵展“文明小卫士”活动,从学生会“督查部”的3名学生(2男1女)中随机选两名进行督导,恰好选中两名男学生的概率是( )
A. |
B. |
C. |
D. |
如图,在菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为( )

| A.1 | B. |
C.2 | D. |
一个口袋中装有4个白色球,1个红色球,7个黄色球,搅匀后随机从袋中摸出1个球是白色球的概率是 .
菱形ABCD的一条对角线长为6cm,边AB的长是方程x2-7x+12=0的一个根,则菱形ABCD的面积为 cm2.
现有四张分别标有1,2,2,3的卡片,它们除数字外完全相同,把卡片背面向上洗匀,从中随机抽取一张后放回,再背面朝上洗匀,从中随机抽出一张,则两次抽出的卡片所标数字不同的概率是 .
如图,在直角坐标系中,△ABC的各顶点坐标为A(-1,1),B(2,3),C(0,3).现以坐标原点为位似中心,作△A′B′C′,使△A′B′C′与△ABC的位似比为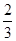 .则点A的对应点A′的坐标为 .
.则点A的对应点A′的坐标为 .
如图,DE∥BC,EF∥CG,AD:AB=1:3,AE=3.
(1)求EC的值;
(2)求证:AD•AG=AF•AB.
如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,求树高AB.
如图,△ABC中,CD是边AB上的高,且 .
.
(1)求证:△ACD∽△CBD;
(2)求∠ACB的大小.
如图,在▱ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F,连接BD.
(1)求证:△ABE≌△CDF;
(2)若AB=DB,求证:四边形DFBE是矩形.
如图,在宽为20米、长为30米的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551米2,则修建的路宽应为多少米?
小明和小刚做游戏,用一个不透明袋子,里面装有形状、大小完全相同的2个红球和2个白球,并充分搅匀,让小刚从中摸出一个球不放回,再去摸第二个球,如果两次摸出的球颜色相同小刚赢,反之小明赢.你认为这种游戏是否公平?请你借助树状图或列表的方法,运用概率的知识予以说明.
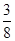
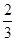


 粤公网安备 44130202000953号
粤公网安备 44130202000953号