江苏省无锡市滨湖区七年级上学期期中考试数学试卷
中国航母辽宁舰是中国人民海军第一艘可以搭载固定翼飞机的航空母舰,满载排水量为67500吨,这个数据用科学记数法表示为( ).
A.6.75×10 吨 吨 |
B.6.75×10 吨 吨 |
C.0.675×10 吨 吨 |
D.67.5×10 吨 吨 |
下列一组数:—8、2.7、—3 、
、 、0.66666…、0.2、0.080080008…,其中无理数的个数为( ).
、0.66666…、0.2、0.080080008…,其中无理数的个数为( ).
| A.0 | B.1 | C.2 | D.3 |
下列合并同类项正确的有( ).
| A.2a+4a=8a2 | B.3x+2y=5xy |
| C.7x2—3x2=4 | D.9a2b—9ba2=0 |
如果|a+2|+(b—1)2="0" 那么代数式(a+b)2015的值是( ).
| A.1 | B.—1 | C.±1 | D.2015 |
若a,b互为相反数,c,d互为倒数, ,则
,则 的值为( ).
的值为( ).
| A.4 | B.—3 | C.1 | D.—3或1 |
下列说法:
①a为任意有理数, +1 总是正数;
+1 总是正数;
②如果 ,则a是负数;
,则a是负数;
③单项式 的系数与次数分别为—4和4;
的系数与次数分别为—4和4;
④代数式 、
、 、
、 都是整式.
都是整式.
其中正确的有( ).
| A.4个 | B.3个 | C.2个 | D.1个 |
如图是计算机程序计算,若开始输入x= —1,则最后输出的结果是( ).

| A.11 | B.—11 | C.12 | D.—12 |
如图,从左到右在每个小格子中填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.若前m个格子中所填整数之和是2014,则m的值为( ).
| 9 |
a |
b |
c |
—5 |
1 |
|
|
… |
|
|
A.2015 B.1008 C.1208 D.2008
比较大小:①0________—0.5,② ________
________ (用“>”或“<”填写)
(用“>”或“<”填写)
规定一种运算法则:a※b=a2+2ab,若(—2)※x=—2+ x,则x=_________.
三个互不相等的有理数,既可以表示为1、a+b、a的形式,又可以表示为0、 、b的形式,
、b的形式,
则a2014+b2015的值_________.
(1)在数轴上把下列各数表示出来: ,
, ,
, ,
,


(2)将上列各数用“<”连接起来:__________________________________________________.
(1)化简:2a-[a-2(a-b)]-b
(2)先化简,再求值:已知多项式A=3 2—6ab+b2,B=—2
2—6ab+b2,B=—2 2+3ab—5b2,当
2+3ab—5b2,当 =1,b=—1时,求A+2B的值.
=1,b=—1时,求A+2B的值.
有理数 <0 、
<0 、 >0 、
>0 、 >0,且
>0,且 .
.
(1)在数轴上将a、b、c三个数填在相应的括号中.
(2)化简: .
.
A、B两个动点在数轴上做匀速运动,它们的运动时间以及位置记录如下.
(1)根据题意,填写下列表格;
| 时间(s) |
0 |
5 |
7 |
x |
| A点位置 |
19 |
—1 |
|
|
| B点位置 |
|
17 |
27 |
|
(2)A、B两点能否相遇,如果相遇,求相遇时的时刻及在数轴上的位置;如果不能相遇,请说明理由;
(3)A、B两点能否相距18个单位长度,如果能,求相距18个单位长度的时刻;如不能,请说明理由.
在计算3+5+7+9+11+13的值时,小明直接计算出结果为48,爱动脑筋的小红,发现这6个数据的特点后,用 的方法来计算,也得出同样的结果.
的方法来计算,也得出同样的结果.
请用上面小红的发现解答下面问题:
某公司对外出租一商铺,符合条件的两商户A、B分别拟定上缴利润方案如下:
A:每年结算一次上缴房租,第一年上缴1.5万元,以后每年比前一年增加1万元;
B:每半年结算一次上缴房租,第一个半年上缴0.3万元,以后每半年比前半年增加0.3万元;
(1)如果承租期限3年,则A商户上缴房租的总金额为 万元,B商户上缴房租的总金额为________万元;
(2)如果承租期限为n年,分别求A、B两商户上缴房租的总金额;(用含n的代数式表示)
(3)如果承租期限n=20时,那么哪个商户上缴房租的总金额比较多?
一张长方形纸片,剪下一个正方形,剩下一个长方形,称为第一次操作;在剩下的长方形纸片中再剪下一个正方形,剩下一个长方形,称为第二次操作;…;若在第 次操作后,剩下的长方形为正方形,则称原长方形为
次操作后,剩下的长方形为正方形,则称原长方形为 阶奇异长方形.如图1,长方形ABCD中,若AB=2,BC=6,则称长方形ABCD为2阶奇异长方形.
阶奇异长方形.如图1,长方形ABCD中,若AB=2,BC=6,则称长方形ABCD为2阶奇异长方形.
(1)判断与操作:如图2,长方形ABCD长为10,宽为4,它是奇异长方形,请写出它是____阶奇异长方形,并在图中画出裁剪线;
(2)探究与计算:已知长方形ABCD的一边长为30,另一边长为a(a<30),且它是3阶奇异长方形,请画出所有可能的长方形ABCD及裁剪线的示意图,并求出相应的 值.
值.






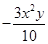 的系数是_______;
的系数是_______;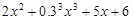 是______次四项式.
是______次四项式. —2=0是一元一次方程,则a= .
—2=0是一元一次方程,则a= . ;
; ;
;  .
. ;
;
 粤公网安备 44130202000953号
粤公网安备 44130202000953号