山东省临沂市九年级上学期阶段性抽测数学试卷

一元二次方程的根是（ ）

下列图形中，中心对称图形有（ ）

关于x的方程的根的情况描述正确的是（ ）

关于x的方程有两个不相等的实根、，且有，则a的值是（ ）

如图，将Rt△ABC（其中∠B=30°，∠C=90°）绕点A按顺时针方向旋转到△AB₁C₁的位置，使得点C、A、B₁在同一条直线上，那么旋转角等于（ ）

A．115°    B．120°    C．125°    D．145°

2011年向阳村农民人均收入为7200元，到2013年增长至8712元．这两年中，该村农民人均收入平均每年的增长率为（ ）

抛物线与x轴的两个交点为（﹣1，0），（3，0），其形状与抛物线相同，则的函数关系式为（ ）

A．

B．

C．

D．

如图，线段AB是⊙O的直径，弦CD丄AB，∠CAB=20°，则∠AOD等于（ ）

如图，△ABC的边AC与⊙O相交于C、D两点，且经过圆心O，边AB与⊙O相切，切点为B．已知∠A=30°，则∠C的大小是（ ）

A．30°    B．45°    C．60°    D．40°

对于二次函数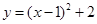的图象，下列说法正确的是（ ）

二次函数（a，b，c为常数，且）中的x与y的部分对应值如下表：

下列结论：
（1）ac＜0；
（2）当x＞1时，y的值随x值的增大而减小．
（3）3是方程的一个根；
（4）当﹣1＜x＜3时，．
其中正确的个数为（ ）

如图，P为⊙O的直径BA延长线上的一点，PC与⊙O相切，切点为C，点D是⊙上一点，连接PD．已知PC=PD=BC．下列结论：
（1）PD与⊙O相切；（2）四边形PCBD是菱形；（3）PO=AB；（4）∠PDB=120°．
其中正确的个数为（ ）

A．4个    B．3个    C．2个    D．1个

若关于x的一元二次方程没有实数根，则k的取值范围是            ．

已知一元二次方程的两根为a与b，则的值是        ．

如图，点A、B、P在⊙O上，∠APB=50°，若M是⊙O上的动点，则等腰△ABM顶角的度数为                            ．

如图所示，在△ABC中，∠B=40°，将△ABC绕点A逆时针旋转至△ADE处，使点B落在BC延长线上的D点处，∠BDA=45°，则∠BDE=          ．

如图所示，在平面直角坐标系xOy中，半径为2的⊙P的圆心P的坐标为（﹣3，0），将⊙P沿x轴正方向平移，使⊙P与y轴相切，则平移的距离为          ．

已知二次函数（）的图象如图所示，给出以下结论：①；②；③；④；⑤．
其中结论正确的是          ．（填正确结论的序号）

解方程：
（1）；              
（2）．

如图，四边形ABCD是正方形，△ADF按顺时针方向旋转一定角度后得到△ABE，若AF=4．AB=7．

（1）旋转中心为        ；旋转角度为          ；
（2）求DE的长度；
（3）指出BE与DF的关系如何？并说明理由．

四边形ABCD是正方形，E、F分别是DC和CB的延长线上的点，且DE=BF，连接AE、AF、EF．

（1）试判断△AEF的形状，并说明理由；
（2）填空：△ABF可以由△ADE绕旋转中心       点，按顺时针方向旋转        度得到；
（3）若BC=8，则四边形AECF的面积为        ．（直接写结果）

如图，AD为△ABC外接圆的直径，AD⊥BC，垂足为点F，∠ABC的平分线交AD于点E，连接BD，CD．

（1）求证：BD=CD；
（2）请判断B，E，C三点是否在以D为圆心，以DB为半径的圆上？并说明理由．

如图，AB是⊙O的直径，点F，C是⊙O上两点，且，连接AC，AF，过点C作CD⊥AF交AF延长线于点D，垂足为D．

（1）求证：CD是⊙O的切线；
（2）若CD=，求⊙O的半径．

某花圃用花盆培育某种花苗，经过实验发现每盆的盈利与每盆的株数构成一定的关系．每盆植入3株时，平均单株盈利3元；以同样的栽培条件，若每盆增加1株，平均单株盈利就减少0.5元．要使每盆的盈利达到10元，每盆应该植多少株？

如图，抛物线经过点（1，﹣4）和（﹣2，5），请解答下列问题：

（1）求抛物线的解析式；
（2）若与x轴的两个交点为A，B，与y轴交于点C．在该抛物线上是否存在点D，使得△ABC与△ABD全等？若存在，求出D点的坐标；若不存在，请说明理由．
注：抛物线的对称轴是．