初中数学圆内接四边形的性质解答题

如图，已知△ABC和△DEF是两个边长都为10cm的等边三角形，且B、D、C、E都在同一条直线上，连接AD、CF．

（1）求证：四边形ADFC是平行四边形；
（2）若BD=3cm，△ABC沿着BE的方向以每秒1cm的速度运动，设△ABC运动的时间为t秒，
①当t为何值时，平行四边形ADFC是菱形?请说明理由；
②平行四边形ADFC有可能是矩形吗?若可能，求出t的值；若不可能，请说明理由。

如图，已知点D在△ABC的BC边上，DE//AC交AB于E，DF//AB交AC于F．

（1）求证：AE=DF；
（2）若添加条件_______，则四边形AEDF是矩形；
若添加条件_______，则四边形AEDF是菱形；
若添加条件_______，则四边形AEDF是正方形．

已知：正方形ABCD.
（1）如图1，点E、点F分别在边 $AB$和 $AD$上，且 $AE=AF$.此时，线段 $BE$、 $DF$的数量关系和位置关系分别是什么？请直接写出结论.
（2）如图2，等腰直角三角形FAE绕直角顶点A顺时针旋转 $\angle \alpha$，当 $0°<\alpha <90°$时，连接 $BE$、 $DF$，此时（1）中结论是否成立，如果成立，请证明；如果不成立，请说明理由.
（3）如图3，等腰直角三角形FAE绕直角顶点A顺时针旋转 $\angle \alpha$，当 $\alpha =90°$时，连接 $BE$、 $DF$，猜想当 $AE$与 $AD$满足什么数量关系时，直线 $DF$垂直平分 $BE$.请直接写出结论.
（4）如图4，等腰直角三角形FAE绕直角顶点A顺时针旋转 $\angle \alpha$，当 $90°<\alpha <180°$时，连接 $BD$、 $DE$、 $EF$、 $FB$得到四边形 $BDEF$，则顺次连接四边形 $BDEF$各边中点所组成的四边形是什么特殊四边形？请直接写出结论.

（11·大连）（本题9分）如图6，等腰梯形ABCD中，AD∥BC，M是BC的中点，求证：∠DAM＝∠ADM．

如图，四边形 $ABCD$是正方形， $△ABE$是等边三角形， $M$为对角线 $BD$（不含B点）上任意一点，将 $BM$绕点 $B$逆时针旋转60°得到BN，连接 $EN、AM、CM.$

（Ⅰ）求证： $△AMB≌△ENB$；
（Ⅱ）①当M点在何处时， $AM＋CM$的值最小；
②当M点在何处时， $AM＋BM＋CM$的值最小，并说明理由；
（Ⅲ）当 $AM＋BM＋CM$的最小值为 $\sqrt{3}+1$时，求正方形的边长.
 

(本题满分8分)

如图，四边形ABCD中，AB=AC=AD，BC=CD，锐角∠BAC的角平分线AE交BC于点E，AF是CD边上的中线，且PC⊥CD与AE交于点P，QC⊥BC与AF交于点Q．求证：四边形APCQ是菱形．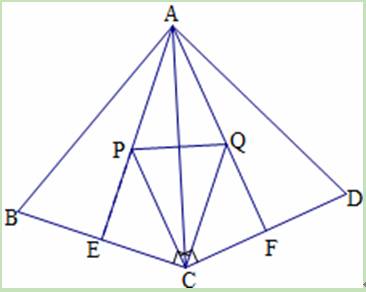

(9分)如图1，在△ABC中，AB=AC，D是底边BC上的一点，BD>CD，将△ABC
沿AD剪开，拼成如图2的四边形ABDC′．
（1）四边形ABDC′具有什么特点？
（2）请同学们在图3中，用尺规作一个以MN，NP为邻边的四边形MNPQ，使四边形MNPQ具有上述特点（要求：写出作法，但不要求证明）．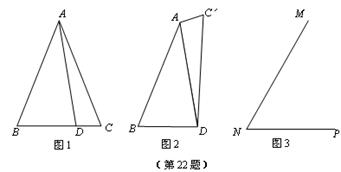

已知矩形ABCD的对角线相交于点O,M 、N分别是OD、OC上异于O、C、D的点。
（1）请你在下列条件①DM=CN,②OM=ON,③MN是△OCD的中位线，④ $MN//AB$中任选一个添加条件（或添加一个你认为更满意的其他条件），使四边形ABNM为等腰梯形，你添加的条件是。
（2）添加条件后，请证明四边形ABNM是等腰梯形。

（本小题满分7分）如图（6），在等腰梯形中，，，
是的中点，连接.、。求证：.

（11·肇庆）(本小题满分8分)
如图8．矩形ABCD的对角线相交于点O．DE∥AC，CE∥BD．
(1)求证：四边形OCED是菱形；
(2)若∠ACB＝30°，菱形OCED的而积为，求AC的长．

（11·肇庆）(本小题满分7分)
如罔7，在一方形ABCD中．E为对角线AC上一点，连接EB、ED，
（1）求证：△BEC≌△DEC：
（2）延长BE交AD于点F，若∠DEB＝140°．求∠AFE的度数．

(8分)在□ABCD中，E、F分别是AB、CD的中点，连接AF、CE．
(1)求证：△BEC≌△DFA；
(2)连接AC，当CA＝CB时，判断四边形AECF是什么特殊四边形？并证明你的结论．

(12分)如图，在矩形ABCD中，AB＝12cm，BC＝8cm．点E、F、G分别从点
A、B、C同时出发，沿矩形的边按逆时针方向移动，点E、G的速度均为2cm/s，点F的速
度为4cm/s，当点F追上点G(即点F与点G重合)时，三个点随之停止移动．设移动开始后
第ts时，△EFG的面积为Scm²．
(1)当t＝1s时，S的值是多少？
(2)写出S与t之间的函数解析式，并指出自变量t的取值范围；
(3)若点F在矩形的边BC上移动，当t为何值时，以点B、E、F为顶点的三角形与以C、F、G为顶点的三角形相似？请说明理由。

如图（图1、图2），四边形ABCD是边长为4的正方形，点E在线段BC上，∠AEF=90°，且EF交正方形外角平分线CP于点F，FN⊥BC，交BC的延长线于点N。
（1）若点E是BC的中点（如图1），AE与EF相等吗？为什么？
（2）点E在BC间运动时（如图2），设BE=x,△ECF的面积为y。
①求y与x的函数关系式；
②当x取何值时，y有最大值，并求出这个最大值。