如图,在直角梯形ABCD中,AD∥BC,BC⊥CD,∠B=60°,BC=2AD,E、F分别为AB、BC的中点.
(1)求证:四边形AFCD是矩形;
(2)求证:DE⊥EF.
(本题12分)如图8,在菱形ABCD中,AE⊥BC,AF⊥CD,垂足为E、F.
(1)求证:△ABE≌△ADF;
(2)若∠BAE=∠EAF,求证:AE=BE;
(3)若对角线BD与AE、AF交于点M、N,且BM=MN(如图9).
求证:∠EAF=2∠BAE.
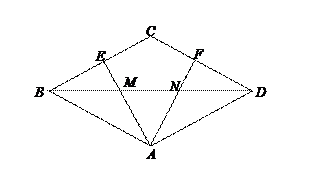
(本题12分)
如图,AD//BC,点E、F在BC上,∠1=∠2,AF⊥DE,垂足为点O.
(1 )求证:四边形AEFD是菱形;
)求证:四边形AEFD是菱形;
(2)若BE=EF=FC,求∠BAD+∠ADC的度数;
(3)若BE=EF=FC,设AB = m,CD = n,求四边形ABCD的面积.
如图,△ABC中,点O在边AB上,过点O作BC的平行线交∠ABC
的平分线于点D,过点B作BE⊥BD,交直线OD于点E。
(1)求证:OE=OD ;
(2)当点O在什么位置时,四边形BDAE是矩形 ?说明理由;
?说明理由;
(3)在满足(2)的条件下,还需△ABC满足什么条件时,四边形BDAE是正方形?写出你确定的条件,并画出图形,不必证明。
如图,平行四边形ABCD中,点E是AD的中点,连接BE并延长交CD的延长线于点F.
(1)求证:△ABE≌△ DFE;
DFE;
(2)连接CE,当CE平分∠BCD时,求证:ED=FD.
已知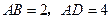 ,
,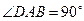 ,
,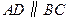 (如图).
(如图).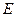 是射线
是射线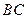 上的动点(点
上的动点(点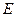 与点
与点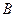 不重合),
不重合),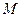 是线段
是线段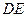 的中点.
的中点.
(1)设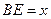 ,
,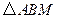 的面积为
的面积为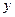 ,求
,求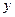 关于
关于 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;
(2)如果以线段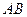 为直径的圆与以线段
为直径的圆与以线段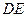 为
为 直径的圆外切,求线段
直径的圆外切,求线段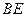 的长;
的长;
(3)连结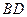 ,交线段
,交线段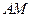 于点
于点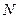 ,如果以
,如果以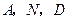 为顶点的三角形与
为顶点的三角形与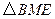 相似,求线段
相似,求线段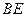 的长.
的长.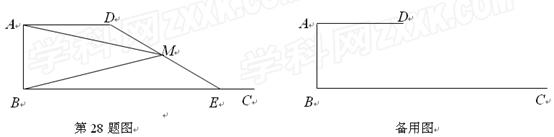
如图,已知:梯形ABCD中,AD∥BC,E为对角线AC的中点,连结
DE并延长交BC于点F,连结AF.
(1)求证:AD=CF;
(2)在原有条件不变的情况下,当AC满足条件 ▲ 时(不再增添辅助线),四边形AFCD成为菱形,
如图,已知D是△ABC的边AB上一点,CE∥AB,DE交 AC于点O,且OA=OC,猜想线段CD与线段AE的大小关系和位置关系,并加以证明.
AC于点O,且OA=OC,猜想线段CD与线段AE的大小关系和位置关系,并加以证明.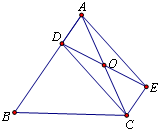
(11·贵港)
如图所示,在梯形ABCD中,AD∥BC,AB=AD,∠BAD的平分线AE交BC于点E,连接DE.
(1)求证:四边形ABED是菱形;
(2)若∠ABC=60°, CE=2BE,试判断△CDE的形状,并说明理由.
CE=2BE,试判断△CDE的形状,并说明理由.
如图,在平行四边形ABCD中,CE = AF. 求证:四边形BEDF是平行四边形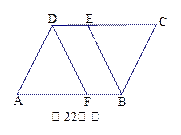
如图,在梯形ABCD中,AD∥BC,BD=CD,AB<CD,且∠ABC为
锐角,AD=4,BC=12,点E为BC上一动点。试求:当CE为何值时,四边形ABED是等腰梯
形?
.如图,四边形ABCD的对角线AC、DB相交于点O,现给出如下三个条件: .
.
(1)请你再增加一个条件:________,使得四边形ABCD为矩形(不添加其它字母和辅助线,只填一个即可,不必证明);
(2)请你从 中选择两个条件________(用序号表示,只填一种情况),使得
中选择两个条件________(用序号表示,只填一种情况),使得 ,并加以证明.
,并加以证明.
四边形ABCD、DEFG都是正方形,连接AE、CG.
(1)求证:AE=CG;
(2)观察图形,猜想AE与CG之间的位置关系,并证明你的猜想.
如图7,菱形ABCD中,E是对角线AC上一点.

(1)求证:△ABE≌△ADE;
(2)若AB=AE,∠BAE=36º,求∠CDE的度数.