2011届南京市玄武区中考数学一模试卷
某工厂第一年生产a件产品,第二年比第一年增产了20%,则该厂两年共生产的
产品件数为
| A.0.2a | B.a | C.1.2a | D.2.2a |
5张完全相同的卡片上,分别画有圆、平行四边形、等边三角形、角、等腰梯形,
现从中随机抽取一张,恰好抽到轴对称图形的概率是
A. |
B. |
C. |
D. |
如图,在□ABCD中,AB = 8,AD = 5,sinA =  ,E是DC上一点,且BE = BC,则DE的长为
,E是DC上一点,且BE = BC,则DE的长为
| A.1 | B.2 | C.3 | D.4 |
如图,△ABC三个顶点的坐标分别为A(2,2),B(4,2),C(6,4),以原
点O为位似中心,将△ABC缩小,使变换后得到的△DEF与△ABC对应边的比为1∶3,
则点C变换后对应的点的坐标为
| A.(3,2) | B.(-3,-2)或(3,2) |
C.(2, ) ) |
D.(2, )或(-2,- )或(-2,- ) ) |
如图,等腰直角△ABC(∠C=90°)的直角边与正方形MNPQ的边长均为4,CA与MN在直线l上,开始时A与M重合,让△ABC向右平移;到C点与N点重合止.设△ABC与正方形MNPQ的重叠部分的面积为ycm2,MA的长度为xcm,则y与x之间的函数关系大致是
“创建文明城,三年上水平”,某市加快了城中村旧房拆迁的步伐.为了解被拆迁的236户家庭对拆迁补偿方案是否满 意,小明利用周末调查了其中的50户家庭,有32户对方案表示满意.在这一抽样调查中,样本容量为 .
如图,在矩形ABCD中,AB<AD,点E在AD上,且CA平分∠BCE.若矩形
ABCD的周长为10,则△CDE的周长为 .
如图,在边长为2的正方形ABCD中,分别以各顶点为圆心在正方形内作四条圆弧,使它们所在的圆外切于点E,F,G,H.则图中阴影部分外围的周长是 (结果保留 ).
).
学校植物园沿路护栏纹饰部分设计成若干个全等菱形图案,每增加一个菱形图案,纹饰长度就增加dcm,如图所示.已知每个菱形图案的边长 cm,其一个内角为60°,若纹饰的总长度L=5030 cm,当d=20时,则需要 个这样的菱形图案.
cm,其一个内角为60°,若纹饰的总长度L=5030 cm,当d=20时,则需要 个这样的菱形图案.
如图,在△ABC中,BC>AC,点D在BC上,且DC=AC.
(1)利用直尺与圆规先作∠ACB的平分线,交AD于F点,再作线段AB的垂直
平分线,交AB于点E,最后连结EF(保留作图痕迹,不要求写作法、证明).
(2)若线段AC= 8,BC= 12,求线段EF的长. 
在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是“摸到白球”的频率折线统计图:
(1)请估计:当 很大时,摸到白球的频率将会接近 (精确到0.01);
很大时,摸到白球的频率将会接近 (精确到0.01);
(2)假如你摸一次,你摸到黑球的概率P(黑球)= ;
(3)试估算盒子里白、黑两种颜色的球各有多 少个?
少个?
(4)在(2)条件下如果要使摸到白球的概率为 ,需要往盒子里再放入多少个白球?
,需要往盒子里再放入多少个白球?
下表是甲地到乙地两条线路的有关数据:
| 线路 |
绕路 |
直路 |
| 路程 |
300公里 |
180公里 |
| 过路费 |
30元 |
90元 |
(1)若小车的平均速度为80公里/小时,则小车走直路比走弯路节省多少时间?
(2)若小车每公里的油耗为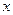 升,按汽油价格为7.5元/升计算,
升,按汽油价格为7.5元/升计算, 设走弯路的总费用为y1,走直路的总费用为y2,问x为何值时,所走哪条线路的总费用较少(总费用=过路费+油耗费);
设走弯路的总费用为y1,走直路的总费用为y2,问x为何值时,所走哪条线路的总费用较少(总费用=过路费+油耗费);
(3)据道路管理部门统计:得到从甲地到乙地的五类不同油耗的小车平均每小时通过的车辆数,制成如图所示的频数分布直方图,请你估算每天早晨7点至晚上5点内这五类小车走直路比走弯路共节省多少升汽油.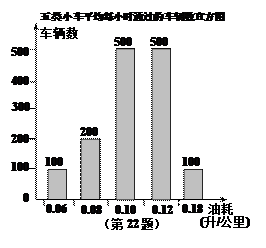
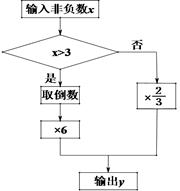
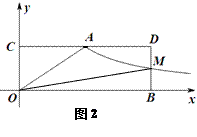
某同学根据图1所示的程序计算后,画出了图2中y与x之间的函数图象,点A在图象上.
(1)结合图1、 图2,求出当0≤x≤3时,y与x之间的函数关系式为________________;当x>3时,y与x之间的函数关系式为________________.
图2,求出当0≤x≤3时,y与x之间的函数关系式为________________;当x>3时,y与x之间的函数关系式为________________.
(2)当y=1.5时,求自变量x的值 .
.
(3)M(m,n)为曲线上一动点,其中m>3,过点M作直线MB∥y轴,交x轴于点B,过点A作直线AC∥x轴交y轴于C,交直线MB于点D.当四边形OADM的面积为6时,判断BM与DM的大小关系,并说明理由.
|
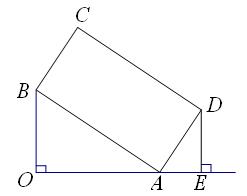
如图,已知OA⊥OB,OA=8,OB=6,以AB为边作矩形ABCD,使AD=a,过点D作DE垂直OA的延长线交于点E.
(1)求证:△OAB∽△EDA;
(2)当a为何值时,△OAB与△EDA全等?并求出此时点C到OE的距离.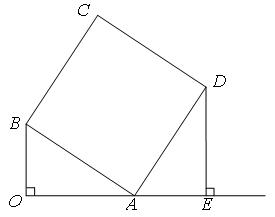
如图,在△ACB中,∠ACB = 90°,AC = 4,BC = 2,点P为射线CA上的一个动点,以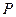 为圆心,1为半径作
为圆心,1为半径作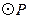 .
.
(1)连结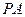 ,若
,若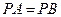 ,试判断
,试判断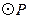 与直线AB的位置关系,并说明理由;
与直线AB的位置关系,并说明理由;
(2)当PC为 时,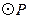 与直线AB相切?当
与直线AB相切?当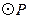 与直线AB相交时,写出PC的取值范围为 ;
与直线AB相交时,写出PC的取值范围为 ;
(3)当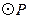 与直线AB相交于点M、N时,是否存在△PMN为正三角形?若存在,求出PC的值;若不存在,说明理由.
与直线AB相交于点M、N时,是否存在△PMN为正三角形?若存在,求出PC的值;若不存在,说明理由.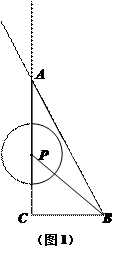
如图,在平面直角坐标系中,抛物线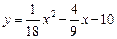 与x轴的右交点为点A,与y
与x轴的右交点为点A,与y
轴的 交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动,线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动,线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
(1)求A,B,C三点的坐标和抛物线的顶点的坐标;
(2)当t为何值时,四边形PQCA为平行四边形?
(3)请说明当0<t<4.5时,△PQF的面积总为定值;
(4)当0≤t≤4.5是否存在△PQF为等腰三角形?当t为何值时,△PQF为等腰三角形?(直接写出结果)
某班6名同学在一次“1分钟仰卧起坐”测试中,成绩分别为(单位:次):39,
45,42,37,41,39.这组数据的众数、中位数分别是
| A.42,37 | B.41,42 | C.39,41 | D.39,40 |
菱形OACB在平面直角坐标系中的位置如图所示,点C的坐标是(6,0),点A
的纵坐标是1,则点B的坐标是
| A.(3,1) | B. |
C. |
D.(1,3) |
如图,矩形ABCD中, ,
, ,点P从点B出发,沿
,点P从点B出发,沿 向终
向终
点D匀速运动,设点P走过的路程为x,△ABP的面积为S,能正确反映S与x之间函数
关系的图象是
A B C D
据上海世博会官方网统计,截至2010年3月29日为止,上海世博会门票已实现销售约22 170 000张.将22 170 000用科学记数法表示为( )
A. |
B. |
C. |
D. |
如图1,修建抽水站时,沿着倾斜角为30°的斜坡铺设管道,若量得水管AB的长度为80米,那么点B离水平面的高度BC的长为( )
A. 米 米 |
B. 米 米 |
C.40米 | D.10米 |
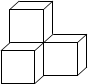
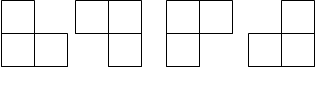
小军将一个直角三角板(如图1)绕它的一条直角边所在的直线旋转一周形成一
个几何体,将这个几何体的侧面展开得到的大致图形是
A  B
B  C
C  D
D 
某班派5名同学参加拔河比赛,他们的体重分别是(单位:千克):67,58, 63,
57, 58,这组数据的中位数为_____▲____.
对于反比例函数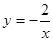 ,下列说法:①点
,下列说法:①点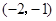 在它的图象上;②它的图
在它的图象上;②它的图
象在第二、四象限;③当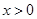 时,
时,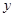 随
随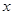 的增大而增大;④当
的增大而增大;④当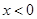 时,
时,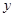 随
随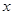 的增大而减小.上述说法中,正确的序号是 ▲ .(填上所有你认为正确的序号)
的增大而减小.上述说法中,正确的序号是 ▲ .(填上所有你认为正确的序号)
在课外活动期间,小英、小丽和小敏在操场上画出A、B两个区域,一
起玩投沙包游戏.沙包落在A区域所得分值与落在B区域所得分值不同.当每人各投沙包
四次时,其落点和四次总分如图所示.请求出小敏的四次总分.
某区老年人、成年人、青少年各年龄段的实际人口比是3:5:2,为了解该地区20万读者对工具书、小说、诗歌、漫画四类图书的喜爱情况,按上述比例随即抽取一定数量的读者进行调查(每人只选一类图书 ),根据调查结果绘制了两幅尚不完整的统计图:
),根据调查结果绘制了两幅尚不完整的统计图:
根据统计图 所提供的信息,完
所提供的信息,完 成下列问题;
成下列问题;
(1)本次共调查了 ▲ 名读者;
(2)补全条形统计图,并计算喜欢小说人数所占的百分比。
(3)估计该地区青少年中喜爱漫画的读者大约有多少名?
如图,平行四边形ABCD中,点E是AD的中点,连接BE并延长交CD的延长线于点F.
(1)求证:△ABE≌△ DFE;
DFE;
(2)连接CE,当CE平分∠BCD时,求证:ED=FD.
在课外活动时间,小王、小丽、小华做“互相踢踺子”游戏,踺子从一人传到另一人就记为踢一次.
(1)若从小丽开始,经过两次踢踺后,踺子踢到小华处的概率是多少?
(2)若从小丽开始踢,经过三次踢踺后,小丽认为踢到她的可能性最大,你同意她的观点吗?请说明理由.
热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为50°热 气球与高楼的水平距离为60 m,这栋高楼有多高?(结果精确到0. 1 m,参考数据:sin50°≈0.78,cos50°≈0.
气球与高楼的水平距离为60 m,这栋高楼有多高?(结果精确到0. 1 m,参考数据:sin50°≈0.78,cos50°≈0. 64 ,tan50°≈1.19 ,
64 ,tan50°≈1.19 , ≈1.73 )
≈1.73 )
如图24,已知抛物线 过点C(3,8),与
过点C(3,8),与 轴交于A,B两点,与y轴交于点D(0,5).
轴交于A,B两点,与y轴交于点D(0,5).
(1)求该二次函数的关系式;
(2)求该抛物线的顶点M的坐标,并求四边形ABMD的面积;
如图,AB为⊙O的直径,点C在上,点D在AB的延长线上于,且AC=CD,已知∠D=30°.
⑴判断CD与⊙O的位置关系,请说明理由。
⑵若弦CF⊥AB,垂足为E,且CF= ,求图中阴影部分的面积.
,求图中阴影部分的面积.
阅读下列材料
将图1的平行四边形用一定方法可分割成面积相等的八个四边形,如图2,再将图2中的八个四边形适当组合拼成两个面积相等且不全等的平行四边形.(要求:无缝隙且不重叠)
请你参考以上做法解决以下问题:
(1)将图4的平行四边形分割成面积相等的八个三角形;
(2)将图5的平行四边形用不同于(1)的分割方案,分割成面积相等的八个三角形,再将这八个三角形适当组合拼成两个面积相等且不全等的平行四边形,类比图2,图3,用数字 1至8标明.
1至8标明.
(3)设每个小格点正方形的边长为1,请你直接写出在(2)中拼成的两个不全等的平行四
边形的周长。
小林家、小华 家与图书馆依次在一条直线上.小林、小华两人同时各自从家沿直线匀速步行到图书馆借阅图书,已知小林到达图书馆花了20分钟。设两人出发x(分钟)后,小林离小华家的距离为y(米),y与x的函数关系如图所示。
家与图书馆依次在一条直线上.小林、小华两人同时各自从家沿直线匀速步行到图书馆借阅图书,已知小林到达图书馆花了20分钟。设两人出发x(分钟)后,小林离小华家的距离为y(米),y与x的函数关系如图所示。
(1)小林的速度为 ▲ 米/分钟 ,a= ▲ ,小林家离图书馆的距离为 ▲ 米;
(2 )已知小华的步行速度是40米/分钟,设小华步行时与家的距离为y1(米),请在图中
)已知小华的步行速度是40米/分钟,设小华步行时与家的距离为y1(米),请在图中
画出y1(米)与x(分钟 )的函数图象;
(3)小华出发几分钟后两人在途中相遇?
|

如图,小明将一张直角梯形纸片沿虚线剪开,得到矩形ABCD和三角形EGF两张纸片,测得AB=5,AD=4,EF= .在进行如下操作时遇到了下面的几个问题,请你帮助解决.
.在进行如下操作时遇到了下面的几个问题,请你帮助解决.
(1) 请你求出FG的长度.
(2)在(1)的条件下,小明先将三角形的边EG和矩形边AB重合,然后将△EFG沿直线BC向右平移,至F点与B重合时停止.在平移过程中,设G点平移的距离为x,两纸片重叠部分面积为.y,求在平移的整个过程中,y与x的函数关系式,并求当重叠部分面积为10时,平移距离x的值.
(3)在(2)的操作中, 小明发现在平移过程中,虽然有时平移的距离不等,但两纸片重叠的面积却是相等的;而有时候平移的距离不等,两纸片重叠部分的面积也 不可能相等.请探索这两种情况下重叠部分面积y的范围(直接写出结果).
小明发现在平移过程中,虽然有时平移的距离不等,但两纸片重叠的面积却是相等的;而有时候平移的距离不等,两纸片重叠部分的面积也 不可能相等.请探索这两种情况下重叠部分面积y的范围(直接写出结果).
 的解集在数轴上表示为 ( )
的解集在数轴上表示为 ( )
 ,则
,则 的值为( )
的值为( ) 的相反数为 .
的相反数为 . 的解是 .
的解是 . ,其中x=2sin60°+1.
,其中x=2sin60°+1.

 的图象位于第二、四象限,则
的图象位于第二、四象限,则 的取值可以是
的取值可以是 的是( )
的是( )










 中自变量x的取值范围是 ▲ .
中自变量x的取值范围是 ▲ .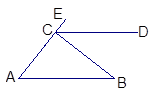
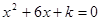 有两个不相等的实数根,则
有两个不相等的实数根,则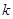 的取值范围是 ____▲____
的取值范围是 ____▲____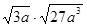 (a≥0)的结果 ▲ .
(a≥0)的结果 ▲ .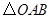 绕点
绕点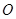 逆时针旋转
逆时针旋转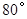 得到
得到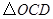 ,若
,若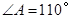 ,
,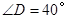 ,则
,则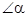 的度数是_______▲________.
的度数是_______▲________.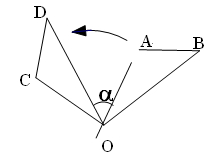

 并写出不等式组的整数解。
并写出不等式组的整数解。 ,其中
,其中 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号