小林家、小华 家与图书馆依次在一条直线上.小林、小华两人同时各自从家沿直线匀速步行到图书馆借阅图书,已知小林到达图书馆花了20分钟。设两人出发x(分钟)后,小林离小华家的距离为y(米),y与x的函数关系如图所示。
家与图书馆依次在一条直线上.小林、小华两人同时各自从家沿直线匀速步行到图书馆借阅图书,已知小林到达图书馆花了20分钟。设两人出发x(分钟)后,小林离小华家的距离为y(米),y与x的函数关系如图所示。
(1)小林的速度为 ▲ 米/分钟 ,a= ▲ ,小林家离图书馆的距离为 ▲ 米;
(2 )已知小华的步行速度是40米/分钟,设小华步行时与家的距离为y1(米),请在图中
)已知小华的步行速度是40米/分钟,设小华步行时与家的距离为y1(米),请在图中
画出y1(米)与x(分钟 )的函数图象;
(3)小华出发几分钟后两人在途中相遇?
|

相关知识点
推荐套卷
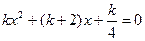 有两个不相等的实数根.
有两个不相等的实数根.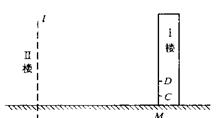
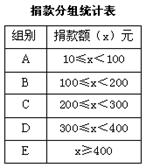
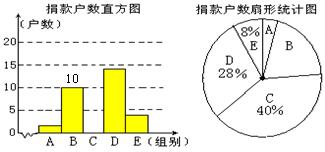
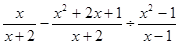 ,其中
,其中 。
。 粤公网安备 44130202000953号
粤公网安备 44130202000953号