如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.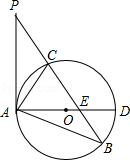
(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG•AB=12,求AC的长;
(3)在满足(2)的条件下,若AF:FD=1:2,GF=1,求⊙O的半径及sin∠ACE的值.
推荐套卷
如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.
(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG•AB=12,求AC的长;
(3)在满足(2)的条件下,若AF:FD=1:2,GF=1,求⊙O的半径及sin∠ACE的值.