2011年初中毕业升学考试(辽宁丹东卷)数学
已知代数式 与
与 是同类项,那么点
是同类项,那么点 在( )
在( )
| A.第一象限 | B.第二象限 | C.第二象限 | D.第四象限 |
一个多边形的内角和是外角和的2倍,则这个多边形的边数为( )
| A.4 | B.5 | C.6 | D.7 |
只用下列正多边形地砖中的一种,能够铺满地面的是( )
A.正五边形 |
B.正六边形 |
C.正八边形 | D.正十边形 |
下列命题:①坐标平面内,点(a,b)与点(b,a)表示同一个点;②要了解一批电视机的使用寿命,从中任意抽取40台电视机进行试验,在这个问题中,样本容量是40台电视机;③过一点有且只有一条直线与这条直线平行;④如果a<b,那么a c < b c;其中真命题有( )
| A.3个 | B.2个 | C.1个 | D.0个 |
若a>0,b<-2,则点(a,b+2)应在( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
某住宅小区六月份中1日至6日每天用水量变化情况如图所示,那么这6天的平均用水量是( )
| A.30吨 | B.31吨 | C.32吨 | D.33吨 |
如图,∠1=∠2,∠E=∠A,EC=DA,则△ABD≌△EBC时,运用的判定定理是( )
| A.SSS | B.ASA | C.AAS | D.SAS |

如图,DE⊥BC,BE=EC,且AB=5,AC=8,则△ABD的周长为( )
| A.21 | B.18 | C.13 | D.9 |

有40个数据,共分成6组,第1~4组的频数分别为10,5,7,6.第5组的频率是0.1,则第6组的频数是________.
某种商品的进价为800元,出售时标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于5%,则至多可打 .
如图 ABC中,AD是BC上的中线,BE是
ABC中,AD是BC上的中线,BE是 ABD中AD边上的中线,若
ABD中AD边上的中线,若 ABC的面积是24,则
ABC的面积是24,则 ABE的面积是________。
ABE的面积是________。
(本题满分8分)如图,点B、E、C、F在一条直线上,BC=EF,AB∥DE,∠A=∠D.
求证:△ABC≌△DEF.
(本题8分)随着我国人民生活水平和质量的提高,百岁寿星日益增多.某市是中国的长寿之乡,截至2008年2月底,该市五个地区的100周岁以上的老人分布如下表(单位:人):
 地区 地区性别 |
一 |
二 |
三 |
四 |
五 |
| 男性 |
21 |
30 |
38 |
42 |
20 |
| 女性 |
39 |
50 |
73 |
70 |
37 |
根据表格中的数据得到条形图如下:
解答下列问题:
(1)请把统计图中地区二和地区四中缺失的数据、图形补充完整;
(2)填空:该市五个地区100周岁以上老人中,男性人数的极差(最大值与最小值的差)是 人,女性人数的最多的是地区______;
(3)预计 2015年该市100周岁以上的老人将比2008年2月的统计数增加100人,请你估算2015年地区一增加100周岁以上的男性老人多少人?
2015年该市100周岁以上的老人将比2008年2月的统计数增加100人,请你估算2015年地区一增加100周岁以上的男性老人多少人?
(本题满分8分)
某中学为八年级寄宿学生安排宿舍,如果每间4人,那么有20人无法安排,如果每间8人,那么有一间不空也不满,求宿舍间数和寄宿学生人数。
(本题满分8分)
我市某化工厂现有甲种原料290千克,乙种原料212千克,计划利用这两种原料生产A、B两种产品共80件,生产一件A产品需要甲种原料5千克 ,乙种原料1.5千克;生产一件B种产品需要甲种原料2.5千克,乙种原料3.5千克,该化工厂现有的原料能否保证生产顺利进行?若能的话,有几种方案?请你设计出来。
,乙种原料1.5千克;生产一件B种产品需要甲种原料2.5千克,乙种原料3.5千克,该化工厂现有的原料能否保证生产顺利进行?若能的话,有几种方案?请你设计出来。
(本题满分10分)
已知:如图,在△ABC中,D为BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于点G,DE⊥GF,并交AB于点E,连结EG.
(1)求证BG=CF;
(2)试猜想BE+CF与EF的大小关系,并加以证明.
(11·丹东)用科学记数法表示310000,结果正确的是 ( )
| A.3.1×104 | B.3.1×105 | C.31×104 | D.0. 31×106 |
(11·丹东)在一个不透明的口袋中装有10个除了颜色外均相同的小球,其中5个红球,3个黑球,2个白球,从中任意摸出一球是红球的概率是 ( )
A. |
B. |
C. |
D. |
(11·丹东)某一时刻,身高1.6m的小明在阳光下的影长是0.4m.同一时刻同一地点,测得某旗杆的影长是5m,则该旗杆的高度是 ( )
| A.1.25m | B.10m | C.20m | D.8m |
(11·丹东)一个正方体的每一个面都有一个汉字,其平面展开图如图所示,那么在该正方体中和“城字”相对的字是 ( )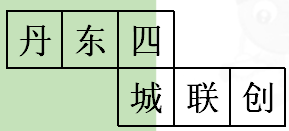
| A.丹 | B.东 | C.创 | D.联 |
(11·丹东)如图,在Rt△ABC中,∠C=90°, BE平分∠ABC,ED垂直平分AB于D,若AC=9,则AE的值是 ( )
A. |
B. |
C.6 | D. 4 |
(11·丹东)一组数据:12,13,15,14,16,18,19,14.则这组数据的极差是____________.
(11·丹东)如图,将半径为3cm的圆形纸片剪掉三分之一,余下部分围成一个圆锥的侧面,则这个圆锥的高是_____________.
(11·丹东)已知:线段AB=3.5cm,⊙A和⊙B的半径分别是1.5cm和4cm,则⊙A和⊙B的位置关系是____________.
(11·丹东)已知:如图,DE是△ABC的中位线,点P是DE的中点,CP的延长线交AB于点Q,那么 ______________.
______________.
(11·丹东)(本题8分)每个小方格是边长为1个单位长度的小正方形,梯形ABCD在平面直角坐标系中的位置如图所示.
(1)在平面直角坐标系中画出梯形ABCD关于直线AD的轴对称图形AB1C1D;
(2)点P是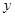 轴上一个动点,请直接写出所有满足△POC是等腰三角形的动点P的坐标.
轴上一个动点,请直接写出所有满足△POC是等腰三角形的动点P的坐标.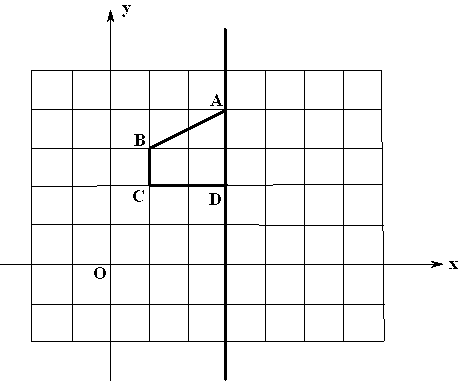
(11·丹东)(本题10分)某学校为了解学生每周在饮料方面的花费情况进行了抽样调查,调查结果制成了条形统计图和扇形统计图.请你结合图中信息完成下列问题:
(1)补全条形图.
(2)本次抽样调查了多少名学生?
(3)请求出抽样调查的数据的平均数,并直接写出中位数和人数.
(4)扇形统计图中,花费20元的人数所在扇形圆心角度数是多少度?
数学课堂上,为了学习构成任意三角形三边需要满足的条件.甲组准备3根本条,长度分别是3cm、8cm、13cm;乙组准备3根本条,长度分别是4cm、6cm、12cm.老师先从甲组再从乙组分别随机抽出一根本条,放在一起组成一组.
(1)用画树状图法(或列表法)分析,并列出各组可能.(画树状图或列表及列出可 能时不用写单位)
能时不用写单位)
(2)现在老师也有一根本条, 长度为5cm,与(1)中各组本条组成三角形的概率是多少?
长度为5cm,与(1)中各组本条组成三角形的概率是多少?
(11·丹东)(本题10分)数学兴趣小组想利用所学的知识了解某广告牌的高度,已知CD=2cm.经测量,得到其它数据如图所示.其中 ,
, ,AB=10cm.请你根据以上数据计算GH的长.
,AB=10cm.请你根据以上数据计算GH的长.
( ,要求结果精确到0.1m)
,要求结果精确到0.1m)
(11·丹东)(本题10分)已知:如图,在 中,
中, ,以AC为直径作⊙O交AB于点D.
,以AC为直径作⊙O交AB于点D.
(1)若 ,求线段BD的长.
,求线段BD的长.
(2)若点E为线段BC的中点,连接DE. 求证:DE是⊙O的切线.
(11·丹东)(本题10分)某文具店老板第一次用1000元购进一批文具,很快销售完毕;第二次购进时发现每件文具进价比第一次上涨了2.5元.老板用2500元购进了第二批文具,所购进文具的数量是第一次购进数量的2倍,同样很快 销售完毕.两批文具的售价均为每件15元.
销售完毕.两批文具的售价均为每件15元.
(1)问第二次购进了多少件文具?
(2)文具店老板在这两笔生意中共盈利多少元?
(11·丹东)(本题10分)某食品加工厂需要一批食品包装盒,供应这种包装盒有两种方案可供选 择:
择:
方案一:从包装盒加工厂直接购买,购买所需的费用 与包装盒数
与包装盒数 满足如图1所示的函数关系.
满足如图1所示的函数关系.
方案二:租赁机器自己加工,所需费用 (包括租赁机器的费用和生产包装盒的费用)与包装盒
(包括租赁机器的费用和生产包装盒的费用)与包装盒 满足如图2所示的函数关系.
满足如图2所示的函数关系.
根据图像回答下列问题:
(1)方案一中每个包装盒的价格是多少元?
(2)方案二中租赁机器的费用是多少元?生产一个包装盒的费用是多少元 ?
?
(3)请分别求出 与
与 的函数关系式.
的函数关系式.
(4)如果你是决策者,你认为应该选择哪种方案更省钱?并说明理由.
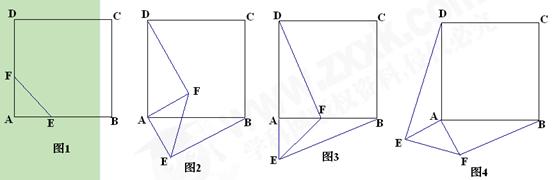
已知:正方形ABCD.
(1)如图1,点E、点F分别在边
和
上,且
.此时,线段
、
的数量关 系和位置关系分别是什么?请直接写出结论.
系和位置关系分别是什么?请直接写出结论.
(2)如图2,等腰直角三角形FAE绕直角顶点A顺时针旋转
,当
时,连接
、
,此时(1)中结论是否成立,如果成立,请证明;如果不成立,请说明理由.
(3)如图3,等腰直角三 角形FAE绕直角顶点A顺时针旋转
,当
时,连接
、
,猜想当
与
满足什么数量关系时,直线
垂直平分
.请直接写出结论.
角形FAE绕直角顶点A顺时针旋转
,当
时,连接
、
,猜想当
与
满足什么数量关系时,直线
垂直平分
.请直接写出结论.
(4)如图4,等腰直角三角形FAE绕直角顶点A顺时针旋转
,当
时,连接
、
、
、
得到四边形
,则顺次连接四边形
各边中点所组成的四边形是什么特殊四边形?请直接写出结论.
 的整数解共有( )
的整数解共有( )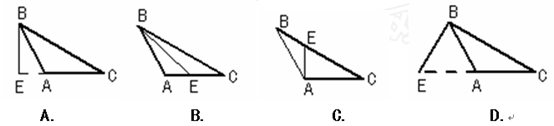
 是二元一次方程组
是二元一次方程组 的解,则
的解,则 的值为( ).
的值为( ).  的解集在数轴上表示为( )
的解集在数轴上表示为( )

 的整数解共有5个,则a的取值范围是 .
的整数解共有5个,则a的取值范围是 . 中,
中, 的平分线相交于点
的平分线相交于点 ,过
,过 等于 .
等于 .








 分解因式,结果正确的是 ( )
分解因式,结果正确的是 ( )



 的图像如图所示,则一次函数
的图像如图所示,则一次函数 的图像大致是( )
的图像大致是( )
 的方差是3,则另一组数据
的方差是3,则另一组数据 的方差是 ( )
的方差是 ( )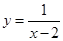 的自变量
的自变量 的取值范围是______________.
的取值范围是______________. 的整数解是 _______________.
的整数解是 _______________.

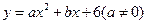 与
与 轴交于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程
轴交于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程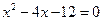 的两个根.
的两个根. 的周长最小,若存在
的周长最小,若存在 ,请求出点P的坐标;若不存在,请说明理由.
,请求出点P的坐标;若不存在,请说明理由. 面积S最大时,求m的值.
面积S最大时,求m的值.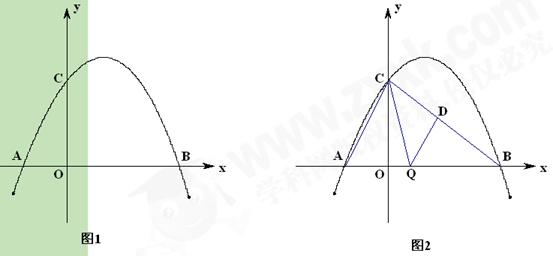
 粤公网安备 44130202000953号
粤公网安备 44130202000953号