(本题满分10分)
已知：如图，在△ABC中，D为BC的中点，过D点的直线GF交AC于F，交AC的平行线BG于点G，DE⊥GF，并交AB于点E，连结EG．
（1）求证BG=CF；
（2）试猜想BE+CF与EF的大小关系，并加以证明．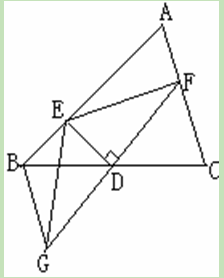
＞1－
．
，并把解集在数轴上表示出来．
；（2）
．相关知识点
推荐套卷
(本题满分10分)
已知：如图，在△ABC中，D为BC的中点，过D点的直线GF交AC于F，交AC的平行线BG于点G，DE⊥GF，并交AB于点E，连结EG．
（1）求证BG=CF；
（2）试猜想BE+CF与EF的大小关系，并加以证明．
粤公网安备 44130202000953号