2011年初中毕业升学考试(湖北黄石卷)数学
(10分 )
)
问题提出
我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小,即要比较代数式M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N;若M-N=0,则M=N;若M-N<0,则M<N.
问题解决
如图1,把边长为a+b(a≠b)的大正方形分割成两个边长分别是a、b的小正方形及两个矩形,试比较两个小正方形面积之和M与两个矩形面积之和N的大小.
解:由图可知:M=a2+b2,N=2ab.
∴M-N=a2+b2-2ab=(a-b)2.
∵a≠b,∴(a-b)2>0.
∴M-N>0.
∴M>N.
类别应用
(1)已知小丽和小颖购买同一种商品的平均价格分别为 元/千克和
元/千克和 元/千克(a、b是正数,且a≠b),试比较小丽和小颖所购买商品的平均价格的高低.
元/千克(a、b是正数,且a≠b),试比较小丽和小颖所购买商品的平均价格的高低.
(2)试比较图2和图3中两个矩形周长M1、N1的大小(b>c).
联系拓广
小刚在超市里买了一些物品,用一个长方体的箱子“打包”,这个箱子的尺寸如图4所示(其中b>a>c>0),售货员分别可按图5、图6、图7三种方法进行捆绑,吻哪种方法用绳最短?哪种方法用绳最长?请说明理由.
(12分)如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,且BD=8cm.点
M从点A出发,沿AC的方向匀速运动,速度为2cm/s;同时直线PQ由点B出发,沿BA
的方向匀速运动,速度为1cm/s,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交
BC于点Q、交BD于点F.连接PM,设运动时间为ts(0<t<5).
(1)当t为何值时,四边形PQCM是平行四边形?
(2)设四边形PQCM的面积为ycm2,求y与t之间的函数关系式;
(3)是否存在某一时刻t,使 ?若存在,求出t的值;若不存在,说明理由;
?若存在,求出t的值;若不存在,说明理由;
(4)连接PC,是否存在某一时刻t,使点M在线段PC的垂直平分线上?若存在,求出此时t 的值;若不存在,说明理由.
的值;若不存在,说明理由.
今年5月,我市第六次人口普查办公室发布了全市常住人口为578.99万人,用科
学记数法可表示(保留2个有效数字)为( )
| A.58×105人 | B.5.8×105人 | C.5.8×106人 | D.0.58×107人 |
下列运算不正确的是( )
| A.a5+a5=2a5 | B.(-2a2)3=-2a6 |
| C.2a2·a-1=2a | D.(2a3-a2)÷a2=2a-1 |
下列事件属于必然事件的是( )
| A.在1个标准大气压下,水加热到100ºC沸腾 | B.明天我市最高气温为56ºC |
| C.中秋节晚上能看到月亮 | D.下雨后有彩虹 |
已知一个菱形的周长是20cm,两条对角线的比为4∶3,则这个菱形的面积是( )
| A.12cm2 | B.24cm2 | C.48cm2 | D.96cm2 |
某小区20户家庭的日用电量(单位:千瓦时)统计如下:
| 日用电量(单位:千瓦时) |
4 |
5 |
6 |
7 |
8 |
10 |
| 户数 |
1 |
3 |
6 |
5 |
4 |
1 |
这20户家庭日用电量的众数、中位数分别是( )
A.6,6.5 B.6,7 C.6,7.5 D.7,7.5
如图,用围棋子按下面的规律摆图形,则摆第n个图形需要围棋子的枚数为( )
| A.5n |
| B.5n-1 |
| C.6n-1 |
| D.2n2+1 |

如图,矩形OABC的顶点O是坐标原点,边OA在x轴上,边OC在y轴上.若
矩形OA1B1C1与矩形OABC关于点O位似,且矩形OA1B1C1的面积等于矩形OABC
面积的 ,则点B1的坐标是( )
,则点B1的坐标是( )
| A.(3,2) | B.(-2,-3) |
| C.(2,3)或(-2,-3) | D.(3,2)或(-3,-2) |
某公园草坪的防护栏由100段形状相同的抛物线形构件组成,为了牢固起见,每
段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这
条防护栏需要不锈钢支柱的总长度至少为( )
| A.50m | B.100m |
| C.160m | D.200m |

如图,圆锥的底面半径OB=10cm,它的侧面展开图的扇形的半径AB=30cm,
则这个扇形圆心角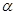 的度数是 .
的度数是 .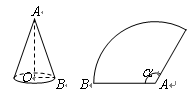
某校举行物理实验操作测试,共准备了三项不同的实验,要求每位学生只参加其
中的一项实验,由学生自己抽签确定做哪项实验.在这次测试中,小亮和大刚恰好做同一
项实验的概率是 .
(8分)今年“世界水日”的主题是“城市用水:应对都市化挑战”.为了解城市
居民用水量的情况,小亮随机抽查了阳光小区50户居民去年每户每月的用水量,将得到的
数据整理并绘制了这50户居民去年每月总用水量的折线统计图和频数、频率分布表如下:
(1)表中a= ,d= .
(2)这50户居民每月总用水量超过550m3的月份占全年月份的百分率是多少(精确到1%)?
(3)请根据折线统计图提供的数据,估计该小区去年每户居民平均月用水量是多少?
(8分)将两块大小相同的含30º角的直角三角板(∠BAC=∠B1A1C=30º)按图1
的方式放置,固定三角板A1B1C,然后将三角板ABC绕直角顶点C顺时针方向旋转(旋转
角小于90º)至图2所示的位置 ,AB与A1C交于点E,AC与A1B1交
,AB与A1C交于点E,AC与A1B1交 于点F,AB与A1B1
于点F,AB与A1B1
交于点O.
(1)求证:△BCE≌△B1CF;
(2)当旋转角等于30º时,AB与A1B1垂直吗?请说明理由.
(8分)被誉为东昌三宝之首的铁塔,始建于北宋时期,是我市现存的最古老的建
筑.铁塔由塔身和塔座两部分组成.为了测得铁 塔的高度,小莹利用自制的测角仪,
塔的高度,小莹利用自制的测角仪, 在C
在C
点测得塔顶E的仰角为45º,在D点测得塔顶E的仰角为60º.已知测角仪AC的高为1.6m,
CD的长为6m,CD所在的水平线CG⊥EF于点G.求铁塔EF的高(精确到0.1m).
(8分)徒骇河风景区建设是今年我市重点工程之一.某工程公司承担了一段河底
清淤任务,需清淤4万方,清淤1万方后,该公司为提高施工进度,又新增一批工程机械参
与施工,工效提高到原来的2倍,共用25天完成任务.问该工程公司新增工程机械 后每天
后每天
清淤多少方?
(8分)如图,AB是半圆的直径,点O是圆心,点C是OA的中点,CD⊥OA交
半圆于点D,点E是的中点,连接AE、OD,过点D作DP∥AE交BA的延长线于点P.
(1)求∠AOD的度数;
(2)求证:PD是半圆O的切线.
黄石市2011年6月份某日一天的温差为11℃,最高气温为t℃,则最低气温可表
示为( )
| A.(11+t)℃ | B.(11-t)℃ | C.(t-11)℃ | D.(-t-11)℃ |
有如下图形:①函数 的图形;②函数
的图形;②函数 的图像;③一段弧;④平行
的图像;③一段弧;④平行
四边形,其中一定是轴对称图形的有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
2010年12月份,某市总工会组织该市各单位参加“迎新春长跑活动”,将报名的
男运动员分成3组:青年组,中年组,老年组。各组人数所占比例如图(2)所示,已知青
年组有120人,则中年组与老年组人数分别是( )
| A.30,10 | B.60,20 | C.50,30 | D.60,10 |

将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶
点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图(3),
则三角板的最大边的长为( )
A. |
B.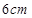 |
C.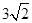 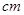 |
D. 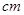 |

平面上不重合的两点确定一条直线,不同三点最多可确定3条直线,若平面上不
同的 个点最多可确定21条直线,则
个点最多可确定21条直线,则 的值为( )
的值为( )
A.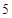 |
B. |
C.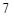 |
D.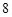 |
已知梯形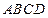 的四个顶点的坐标分别为
的四个顶点的坐标分别为 ,
, ,
, ,
,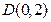 ,
,
直线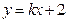 将梯形分成面积相等的两部分,则
将梯形分成面积相等的两部分,则 的值为( )
的值为( )
A. |
B. |
C.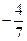 |
D. |
为响应“红歌唱响中国”活动,某乡镇举行了一场“红歌”歌咏比赛,组委会规
定:任何一名参赛选手的成绩 满足:
满足: ,赛后整理所有参赛选手的成绩如表(一)
,赛后整理所有参赛选手的成绩如表(一)
根据表(一)提供的信息得到 .
.
有甲、乙两张纸条,甲纸条的宽是乙纸条宽的2倍,如图(4)。将这两张纸条交
叉重叠地放在一起,重合部分为四边形 ,则
,则 与
与 的数量关系为 .
的数量关系为 .
初三年级某班有54名学生,所在教室有6行9列座位,用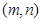 表示第
表示第 行第
行第 列的座位,新学期准备调整座位,设某个学生原来的座位为
列的座位,新学期准备调整座位,设某个学生原来的座位为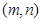 ,如果调整后的座位为
,如果调整后的座位为 ,则称该生作了平移[
,则称该生作了平移[ ]
] ,并称
,并称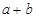 为该生的位置数。若某生的位
为该生的位置数。若某生的位
置数为 ,则当
,则当 取最小值时,
取最小值时,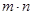 的最大值为 .
的最大值为 .
(本小题满分8分)2011年6月4日,李娜获得法网公开赛的冠军,圆了中国人
的网球梦,也在国内掀起一股网球热。某市准备为青少年举行一次网球知识讲座,小明和妹
妹都是网球球迷,要求爸爸去买门票,但爸爸只买回一张门票,那么谁去就成了问题,小明
想到一个办法:他拿出一个装有质地、大小相同的 个红球与
个红球与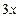 个白球的袋子,让爸爸摸
个白球的袋子,让爸爸摸
出一个球,如果摸出的是红球,妹妹去听讲座,如果摸出的是白球,小明去听讲座。
(1)爸爸说这个办法不公平,请你用概率的知识解释原因。
(2)若爸爸从袋中取出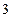 个白球,再用小明提出的办法来确定谁去听讲座,请问摸球的结果是对小明有利还是对妹妹有利,说明理由。
个白球,再用小明提出的办法来确定谁去听讲座,请问摸球的结果是对小明有利还是对妹妹有利,说明理由。
(本小题满分8分)东方山是鄂东南地区的佛教圣地,月亮山是黄荆山脉第二高峰,
山顶上有黄石电视塔。据黄石地理资料记载:东方山海拔453.20米,月亮山海拔442.00米,
一飞机从东方山到月亮山方向水平飞行,在东方山山顶 的正上方
的正上方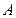 处测得月亮山山顶
处测得月亮山山顶 的
的
俯角为 ,在月亮山山顶
,在月亮山山顶 的正上方
的正上方 处测得东方山山顶
处测得东方山山顶 处的俯角为
处的俯角为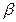 ,如图(7)。已知
,如图(7)。已知 ,若飞机的飞行速度为180米/秒,则该飞机从
,若飞机的飞行速度为180米/秒,则该飞机从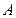 到
到 处
处
需多少时间?(精确到0.1秒)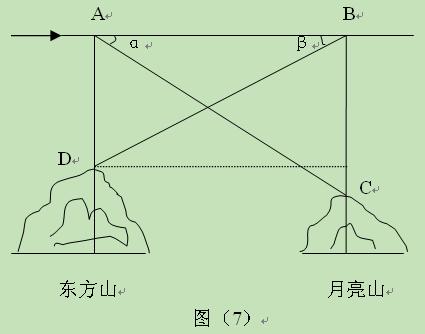
今年,号称"千湖之省"的湖北正遭受大旱,为提高学生环
境意识,节约用水,某校数学教师编制了一道应用题:为了保护水资源,某市制定一套节水
的管理措施,其中对居民生活用水收费作如下规定:
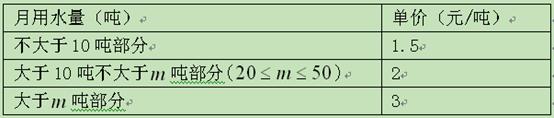
(1)若某用户六月份用水量为
吨,求其应缴纳的水费;
(2)记该用户六月份用水量为
吨,缴纳水费为
元,试列出
与
的函数式;
(3)若该用户六月份用水量为40吨,缴纳水费
元的取值范围为
的取值范围。
各位同学,请你也认真做一做,相信聪明的你一定会顺利完成。
(本小题满分9分)已知⊙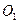 与⊙
与⊙ 相交于
相交于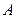 、
、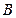 两点,点
两点,点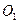 在⊙
在⊙ 上,
上, 为⊙
为⊙ 上一点(不与
上一点(不与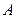 ,
,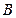 ,
,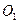 重合),直线
重合),直线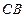 与⊙
与⊙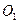 交于另一点
交于另一点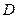 。
。
(1)如图(8),若 是⊙
是⊙ 的直径,求证:
的直径,求证: ;
;
(2)如图(9),若 是⊙
是⊙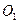 外一点,求证:
外一点,求证: ;
;
(3)如图(10),若 是⊙
是⊙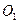 内一点,判断(2)中的结论是否成立。
内一点,判断(2)中的结论是否成立。







 的值为( )
的值为( )
 的图像经过第二、四象限,则
的图像经过第二、四象限,则 的取值范围是( )
的取值范围是( )
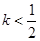



 的两根分别为
的两根分别为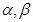 ,且
,且 ,则
,则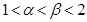


 且
且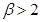
 = .
= . 内接于⊙
内接于⊙ ,若
,若 =30°,
=30°, ,则⊙
,则⊙
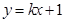 的图像与反比例函数
的图像与反比例函数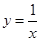 的图像没有公共点,则实数
的图像没有公共点,则实数 的
的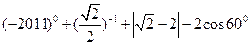
 ,其中
,其中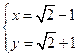 .
. 中,
中, ,
, ,
, 是
是 的中点,连接.
的中点,连接.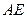 、
、 。求证:
。求证: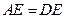 .
.


 时,函数值
时,函数值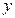 随
随 的增大而减小,求
的增大而减小,求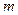 的取值范围。
的取值范围。 为一个顶点作该抛物线的内接正三角形
为一个顶点作该抛物线的内接正三角形 (
( ,
, 两点在抛物线上),请问:△
两点在抛物线上),请问:△
 粤公网安备 44130202000953号
粤公网安备 44130202000953号