如图,E是正方形ABCD的边BC延长线上的点,且CE=AC.
(1)求∠ACE、∠CAE的度数;
(2)若AB=3cm,请求出△ACE的面积.
如图1,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
(1)求证:△DEC≌△EDA;
(2)求DF的值;
(3)如图2,若P为线段EC上一动点,过点P作△AEC的内接矩形,使其顶点Q落在线段AE上,定点M、N落在线段AC上,当线段PE的长为何值时,矩形PQMN的面积最大?并求出其最大值.
已知在△ABC中,∠BAC=90°;分别以AB,BC为边作正方形ABDE和正方形BCFG,连接DC,GA交于点P,求证:PD⊥PG.
如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D、E两点的坐标.
如图,已知正方形ABCD中,边长为10厘米,点E在AB边上,BE=6厘米.
(1)如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPE与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPE与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿正方形ABCD四边运动,求经过多长时间点P与点Q第一次在正方形ABCD边上的何处相遇?
如图,长方形纸片 中,AB=10,将纸片折叠,使顶点
中,AB=10,将纸片折叠,使顶点 落在边
落在边 上的
上的 点处,折痕的一端
点处,折痕的一端 点在边
点在边 上.
上.

图(2)
(1)如图(1),当折痕的另一端 在
在 边上且AE=5时,求AF的长
边上且AE=5时,求AF的长
(2)如图(2),当折痕的另一端 在
在 边上且BG=13时,求AF的长.
边上且BG=13时,求AF的长.
如图,四边形ABCD和ECGF都是正方形.
(1)写出表示阴影部分面积的代数式;(结果要求化简)
(2)当a=4时,求阴影部分的面积.
如图1,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.
(1)在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标;
(2)如图2,若AE上有一动点P(不与A,E重合)自A点沿AE方向E点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为t秒(0<t<5),过P点作ED的平行线交AD于点M,过点M作AE平行线交DE于点N.求四边形PMNE的面积S与时间t之间的函数关系式;当t取何值时,s有最大值,最大值是多少?
(3)在(2)的条件下,当t为何值时,以A,M,E为顶点的三角形为等腰三角形,并求出相应的时刻点M的坐标?
如图,在矩形ABCD中,AB=6,BC=8,动点P以2个单位/秒的速度从A点出发,沿对角线AC向C移动,同时动点Q以1个单位/秒的速度从C点出发,沿CB向点B移动,当其中有一点到达终点时,它们都停止移动.设移动的时间为t秒.
(1)求△CPQ的面积S与时间t之间的函数关系式;
(2)以P为圆心,PA为半径的圆与以Q为圆心,QC为半径的圆相切时,求出t的值.
(3)在P、Q移动的过程中,当△CPQ为等腰三角形时,直接写出t的值;
如图1是矩形纸片ABCD连续两次对折展开平铺后的图形,折痕分别为EF,MN,GH.
(1)如图2,连接BD,与折痕GH,EF,MN分别交于点S,O,T,求证:OE=OF;
(2)如图3,连接ET并延长CD交于点Q,连接FS并延长AB交于点P,连接EP,FQ.求证:四边形EPFQ是菱形;
(3)若四边形EPFQ是正方形,则矩形ABCD需满足的条件是______.
如图,在菱形ABCD中,对角线AC与BD相交于点O.CE∥BD,DE∥AC,连接OE.
求证:OE=AD.
如图,在Rt△ABC中,∠B=90°,AC=60,AB=30.D是AC上的动点,过D作DF⊥BC于F,过F作FE∥AC,交AB于E.设CD=x,DF=y.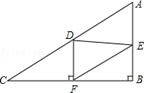
(1)求y与x的函数关系式;
(2)当四边形AEFD为菱形时,求x的值;
(3)当△DEF是直角三角形时,求x的值.