如图1，矩形ABCD中，AB=4，AD=3，把矩形沿直线AC折叠，使点B落在点E处，AE交CD于点F，连接DE．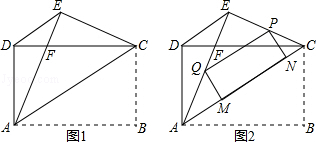
（1）求证：△DEC≌△EDA；
（2）求DF的值；
（3）如图2，若P为线段EC上一动点，过点P作△AEC的内接矩形，使其顶点Q落在线段AE上，定点M、N落在线段AC上，当线段PE的长为何值时，矩形PQMN的面积最大？并求出其最大值．
相关试题
如图所示，矩形ABCD中，AB=6，BC=4，点F在DC上，DF=2．动点M、N分别从点D、B同时出发，沿射线DA、线段BA向点A的方向运动（点M可运动到DA的延长线上），当动点N运动到点A时，M、N两点同时停止运动．连接FM、MN、FN，过ΔFMN三边的中点作ΔPQW．设动点M、N的速度都是1个单位/秒，M、N运动的时间为x秒．试解答下列问题：
（1）说明ΔFMN∽ΔQWP；
（2）设0≤x≤4．试问x为何值时，ΔPQW为直角三角形？
（3）试用含的代数式表示MN2，并求当x为何值时，MN2最小？求此时MN2的值．
推荐套卷
粤公网安备 44130202000953号