如图，在矩形ABCD中，AB=6，BC=8，动点P以2个单位/秒的速度从A点出发，沿对角线AC向C移动，同时动点Q以1个单位/秒的速度从C点出发，沿CB向点B移动，当其中有一点到达终点时，它们都停止移动．设移动的时间为t秒．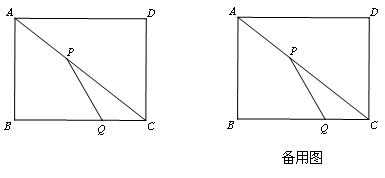
（1）求△CPQ的面积S与时间t之间的函数关系式；
（2）以P为圆心，PA为半径的圆与以Q为圆心，QC为半径的圆相切时，求出t的值．
（3）在P、Q移动的过程中，当△CPQ为等腰三角形时，直接写出t的值；
相关试题
（本小题满分7分）如图，在平面直角坐标系xOy中，函数
的图象
是第二、四象限的角平分线．
（1）实验与探究：由图观察易知A（－1，3）关于直线的对称点
的坐标为（－3，1），请你写出点B（5,3）关于直线的对称点
的坐标为 ；
（2）归纳与发现：结合图形，自己选点再试一试，通过观察点的坐标，你会发现：坐标平面内任一点P（m ,n）关于第二、四象限的角平分线的对称点
的坐标为 ；
（3）运用与拓广：已知两点C（6 , 0），D（2 , 4），试在直线上确定一点，使这点到C，D两点的距离之和最小，在图中画出这点的位置，保留作图痕迹，并求出这点的坐标．
（本小题满分7分）甲、乙两人沿同一路线登山，图中线段
、折线
分别是甲、乙两人登山的路程
（米）与登山时间
之间的函数图象．请根据图象所提供的信息，解答如下问题： 
（1）求甲登山的路程与登山时间之间的函数关系式，并写出自变量的取值范围；
（2）求乙出发后多长时间追上甲？此时乙所走的路程是多少米？
中，
，
相交于点
，
为
的中点，
．
的度数；
，求
的长．
（t）
相关知识点
推荐套卷
粤公网安备 44130202000953号