初中数学圆内接四边形的性质解答题

如图，在中，，是上一点，经过点、、，交于点，过点作，交于点．

求证：（1）四边形是平行四边形；

（2）．

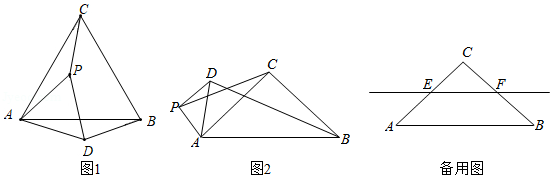
定义：有一组邻边相等且对角互补的四边形叫做等补四边形．

理解：

（1）如图1，点，，在上，的平分线交于点，连接，．

求证：四边形是等补四边形；

探究：

（2）如图2，在等补四边形中，，连接，是否平分？请说明理由．

运用：

（3）如图3，在等补四边形中，，其外角的平分线交的延长线于点，，，求的长．

四边形 $\mathit{ABCD}$ 是 $\odot O$ 的圆内接四边形，线段 $\mathit{AB}$ 是 $\odot O$ 的直径，连结 $\mathit{AC}$ 、 $\mathit{BD}$ ．点 $H$ 是线段 $\mathit{BD}$ 上的一点，连结 $\mathit{AH}$ 、 $\mathit{CH}$ ，且 $\angle \mathit{ACH}=\angle \mathit{CBD}$ ， $\mathit{AD}=\mathit{CH}$ ， $\mathit{BA}$ 的延长线与 $\mathit{CD}$ 的延长线相交于点 $P$ ．

（1）求证：四边形 $\mathit{ADCH}$ 是平行四边形；

（2）若 $\mathit{AC}=\mathit{BC}$ ， $\mathit{PB}=\sqrt{5}\mathit{PD}$ ， $\mathit{AB}+\mathit{CD}=2(\sqrt{5}+1)$

①求证： $\mathit{\Delta DHC}$ 为等腰直角三角形；

②求 $\mathit{CH}$ 的长度．

如图，在中，是斜边的中点，以为直径作圆交于点，延长至，使，连接、，交圆于点．

（1）判断四边形的形状，并说明理由；

（2）求证：；

（3）若，，求的长．

在中，，．点是平面内不与点，重合的任意一点．连接，将线段绕点逆时针旋转得到线段，连接，，．

（1）观察猜想

如图1，当时，的值是　　，直线与直线相交所成的较小角的度数是　　．

（2）类比探究

如图2，当时，请写出的值及直线与直线相交所成的较小角的度数，并就图2的情形说明理由．

（3）解决问题

当时，若点，分别是，的中点，点在直线上，请直接写出点，，在同一直线上时的值．

如图，在 $\text{Rt}\Delta \text{ABC}$ 中， $\angle \mathit{ABC}=90°$ ，点 $M$ 是 $\mathit{AC}$ 的中点，以 $\mathit{AB}$ 为直径作 $\odot O$ 分别交 $\mathit{AC}$ ， $\mathit{BM}$ 于点 $D$ ， $E$ ．

（1）求证： $\mathit{MD}=\mathit{ME}$ ；

（2）填空：

①若 $\mathit{AB}=6$ ，当 $\mathit{AD}=2\mathit{DM}$ 时， $\mathit{DE}=$ 　 　；

②连接 $\mathit{OD}$ ， $\mathit{OE}$ ，当 $\angle A$ 的度数为 　 　时，四边形 $\mathit{ODME}$ 是菱形．

如图， $\mathit{\Delta ABC}$ 内接于圆 $O$ ，且 $\mathit{AB}=\mathit{AC}$ ，延长 $\mathit{BC}$ 到点 $D$ ，使 $\mathit{CD}=\mathit{CA}$ ，连接 $\mathit{AD}$ 交圆 $O$ 于点 $E$ ．

（1）求证： $\mathit{\Delta ABE}\cong \mathit{\Delta CDE}$ ；

（2）填空：

①当 $\angle \mathit{ABC}$ 的度数为 　　时，四边形 $\mathit{AOCE}$ 是菱形．

②若 $\mathit{AE}=\sqrt{3}$ ， $\mathit{AB}=2\sqrt{2}$ ，则 $\mathit{DE}$ 的长为 　　．

如图，已知一张长方形纸片ABCD，AB∥CD ，AD=BC=1，AB=CD=5．在长方形ABCD的边AB上取一点M，在CD上取一点N，将纸片沿MN折叠，使MB与DN交于点K，得到△MNK．

（1）请你动手操作，判断△MNK的形状一定是                  ；
（2）问△MNK的面积能否小于？试说明理由；
（3）如何折叠能够使△MNK的面积最大？请你用备用图探究可能出现的情况，并求最大值．

如图，OABC是一张放在平面直角坐标系中的长方形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=10，OC=8，在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处，求D、E两点的坐标．

如图，平行四边形ABCD（两组对边平行且相等）的边长AB=4，BC=2，若把它放在直角坐标系内，使AB在x轴上，点C在y轴上，点A的坐标是（-3，0），求点B、C、D的坐标．

已知：如图，线段a．求作：正方形ABCD，使正方形ABCD的对角线AC=a．

如图，在正方形ABCD中，E、F分别是边AD、CD上的点，，连接EF并延长交BC的延长线于点G．

（1）求证：△ABE∽△DEF；
（2）若正方形的边长为4，求BG的长．

如图，已知∠AOB，OA=OB，点E在OB边上，四边形AEBF是平行四边形，请你只用无刻度的直尺在图中画出∠AOB的平分线．（保留作图痕迹，不要求写作法）并请说明画出的线为什么平分∠AOB？

如图，在平面直角坐标系中，直线y=0．5x+2与x轴、y轴分别交于A、B两点，以AB为边在第二象限内作正方形ABCD，过点D作DE⊥x轴，垂足为E．

（1）求点A、B的坐标，并求边AB的长；
（2）求点D的坐标；
（3）你能否在x轴上找一点M，使△MDB的周长最小？如果能，请求出M点的坐标；如果不能，说明理由．

在各个内角都相等的多边形中，一个外角等于一个内角的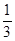．求多边形的边数．