定义：有一组邻边相等且对角互补的四边形叫做等补四边形．
理解：
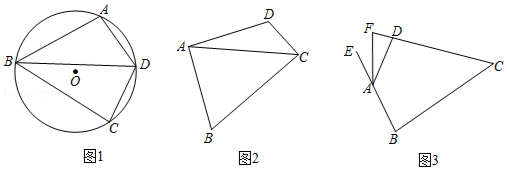
（1）如图1，点，，在上，的平分线交于点，连接，．
求证：四边形是等补四边形；
探究：
（2）如图2，在等补四边形中，，连接，是否平分？请说明理由．
运用：
（3）如图3，在等补四边形中，，其外角的平分线交的延长线于点，，，求的长．
处，在渠岸
的何处开挖才能使所挖水沟最短？
还少6º，求这个角。
相关知识点
推荐套卷
定义：有一组邻边相等且对角互补的四边形叫做等补四边形．
理解：
（1）如图1，点，，在上，的平分线交于点，连接，．
求证：四边形是等补四边形；
探究：
（2）如图2，在等补四边形中，，连接，是否平分？请说明理由．
运用：
（3）如图3，在等补四边形中，，其外角的平分线交的延长线于点，，，求的长．
粤公网安备 44130202000953号