初中数学圆内接四边形的性质试题

在平面直角坐标系xOy中，直线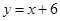与x轴交于点A，与y轴交于点B．

（1）求∠BAO的度数；
（2）如图1，P为线段AB上一点，在AP上方以AP为斜边作等腰直角三角形APD．点Q在AD上，连结PQ，过作射线PF⊥PQ交x轴于点F，作PG⊥x轴于点G．
求证：PF＝PQ ；
（3）如图2，E为线段AB上一点，在AE上方以AE为斜边作等腰直角三角形AED．若P为线段EB的中点，连接PD、PO，猜想线段PD、PO有怎样的关系？并说明理由．

如图，已知正方形ABCD，点E是BC上一点，以AE为边作正方形AEFG。

（1）连结GD，求证△ADG≌△ABE；
（2）连结FC，求证∠FCN=45°；
（3）请问在AB边上是否存在一点Q，使得四边形DQEF是平行四边形？若存在，请证明；若不存在，请说明理由。

如图1，矩形MNPQ中，点E，F，G，H分别在NP，PQ，QM，MN上，若，则称四边形EFGH为矩形MNPQ的反射四边形．图2，图3，图4中，四边形ABCD为矩形，且，．
理解与作图：
（1）在图2，图3中，点E，F分别在BC，CD边上，试利用正方形网格在图上作出矩形ABCD的反射四边形EFGH．
计算与猜想：
（2）求图2，图3中反射四边形EFGH的周长，并猜想矩形ABCD的反射四边形的周长是否为定值？
启发与证明：
（3）如图4，为了证明上述猜想，小华同学尝试延长GF交BC的延长线于M，试利用小华同学给我们的启发证明（2）中的猜想．

如图，矩形ABCD中，AB＝4cm，BC＝8cm，动点M从点D出发，按折线DCBAD方向以2cm/s的速度运动，动点N从点D出发，按折线DABCD方向以1cm/s的速度运动．
（1）若动点M、N同时出发，经过几秒钟两点相遇？
（2）若点E在线段BC上，且BE＝3cm，若动点M、N同时出发，相遇时停止运动，经过几秒钟，点A、E、M、N组成平行四边形？

如图，等腰梯形中，AB∥DC，AD＝BC=5，DC=7，AB=13，动点P从点A出发，以每秒2个单位的速度沿AD→DC→CB→BA向终点A运动，同时点Q从点B出发，以每秒1个单位的速度沿BA向终点A运动，设运动时间为t秒。

⑴求梯形的高为多少？
⑵分段考虑，当t为何值时，四边形PQBC为平行四边形时？
⑶在整个运动过程中，是否存在某一时刻，与重合？

把长方形纸条沿，同时折叠，、两点恰好都落在边的点处，若，，，则长方形的面积为多少？

如图，在梯形ABCD中，AD∥BC，AB＝5，AD＝6，DC＝4，∠C＝45º. 动点M从B点出发沿线段BC以每秒1个单位长度的速度向终点C运动；动点N同时从C点出发沿C→D→A运动，在CD上的速度为每秒个单位长度，在DA上的速度为每秒1个单位长度，当其中一个点到达终点是另一个点也随之停止运动.设运动的时间为t秒．

（1）求BC的长．
（2）当四边形ABMN是平行四边形时，求t的值．
（3）试探究：t为何值时，△ABM为等腰三角形．

如图，已知平行四边形ABCD，

（1）试用三种方法将它分成面积相等的两部分。（保留作图痕迹，不写作法）
（2）由上述方法，你能得到什么一般性的结论？
（3）解决问题：有兄弟俩分家时，原来共同承包的一块平行四边形田地ABCD，现要进行平均划分，由于在这块地里有一口井P，如图所示，为了兄弟俩都能方便使用这口井，兄弟俩在划分时犯难了，聪明的你能帮他们解决这个问题吗？（保留作图痕迹，不写作法）

我们发现，用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题这种方法称为等面积法，这是一种重要的数学方法．请你用等面积法来探究下列两个问题：

（1）如图1是著名的赵爽弦图，由四个全等的直角三角形拼成，请你用它来验证勾股定理；
（2）如图2，在Rt△ABC中，∠ACB=90°，CD是AB边上的高，AC= 4，BC=3，求CD的长度．

如图，梯形ABCD中，AD//BC，AB=CD，对角线AC、BD交于点O，ACBD，E、F、G、H分别为AB、BC、CD、DA的中点.
（1）求证：四边形EFGH为正方形；
（2）若AD=4，BC=6，求四边形EFGH的面积.

在梯形ABCD中，AB∥CD，AC⊥BD，且AC=5，BD=12，则梯形中位线长是_______。

如图①所示，已知A、B为直线l上两点，点C为直线l上方一动点，连接AC、BC，分别以AC、BC为边向△ABC外作正方形CADF和正方形CBEG，过点D作DD₁⊥l于点D₁，过点E作EE₁⊥l于点E₁

（1）如图②，当点E恰好在直线l上时（此时E₁与E重合），试说明DD₁=AB；
（2）在图①中，当D、E两点都在直线l的上方时，试探求三条线段DD₁、EE₁、AB之间的数量关系，并说明理由；
（3）如图③，当点E在直线l的下方时，请直接写出三条线段DD₁、EE₁、AB之间的数量关系．（不需要证明）

阅读下面材料，再回答问题：
有一些几何图形可以被某条直线分成面积相等的两部分，我们将“把一个几何图形分成面积相等的两部分的直线叫做该图形的二分线”，如：圆的直径所在的直线是圆的“二分线”，正方形的对角线所在的直线是正方形的“二分线”。
解决下列问题：
（1）菱形的“二分线”可以是                                   。
（2）三角形的“二分线”可以是                                 。
（3）在下图中，试用两种不同的方法分别画出等腰梯形ABCD的“二分线”.

如图，在等腰梯形ABCD中，AB∥DC，AB＝8cm，CD＝2cm，AD＝6cm。点P从点A出发，以2cm/s的速度沿AB向终点B运动；点Q从点C出发，以1cm/s的速度沿CD、DA向终点A运动（P、Q两点中，有一个点运动到终点时，所有运动即终止）．设P、Q同时出发并运动了t秒。

（1）当PQ将梯形ABCD分成两个直角梯形时，求t的值；
（2）试问是否存在这样的t，使四边形PBCQ的面积是梯形ABCD面积的一半？若存在，求出这样的t的值，若不存在，请说明理由。

如图，在等腰梯形ABCD中，AD∥BC，AB＝DC＝5，AD＝6，BC＝12.动点P从D点出发沿DC以每秒1个单位的速度向终点C运动，动点Q从C点出发沿CB以每秒2个单位的速度向B点运动．两点同时出发，当P点到达C点时，Q点随之停止运动．

(1)梯形ABCD的面积等于________；
(2)当PQ∥AB时，P点离开D点的时间等于______秒；
(3)当P、Q、C三点构成直角三角形时，P点离开D点多长时间？