初中数学圆内接四边形的性质试题

如图，正方形ABCD的面积为18 ，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一动点P，则PD+PE的最小值为__________．

如图，从边长为（a＋4）cm的正方形纸片中剪去一个边长为cm的正方形，剩余部分沿虚线又剪拼成一个矩形（不重叠无缝隙），则矩形的面积（    ）

A．	B．
C．	D．

(1)按语句作图并回答：
作线段AC(AC=4)，以A为圆心a为半径作圆，再以C为圆心b为半径作圆(,,圆A与圆C交于B、D两点)，连结AB、BC、CD、DA．若能作出满足要求的四边形ABCD,则应满足什么条件？
　(2)若，求四边形ABCD的面积.

如图，已知平行四边形ABCD，过A作AM⊥BC于M，交BD于E，过C作CN⊥AD于N，交BD于F，连结AF、CE．
(1)求证：四边形AECF为平行四边形；
(2)当AECF为菱形，M点为BC的中点时，求AB：AE的值．

将矩形纸片ABCD按如图所示的方式折叠，AE、EF为折痕，∠BAE=30°，EB= 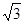，折叠后，点C落在AD边上的C₁处，并且点B落在EC₁边上的B₁处．则BC的长为（　　）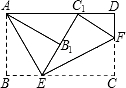

正方形ABCD，矩形EFGH均位于第一象限内，它们的边平行于x轴或y轴，其中，点A，E在直线OM上，点C，G在直线ON上，O为坐标原点，点A的坐标为（3，3），正方形ABCD的边长为1．若矩形EFGH的周长为10，面积为6，则点F的坐标为          .

已知四边形的对角线互相垂直，则顺次连接该四边形各边中点所得的四边形是       (      )

A．梯形

B．矩形

C．菱形

D．正方形

已知一个四边形的对角线互相垂直，那么顺次连接这个四边形的四边中点所得的四边形是

A．矩形

B．菱形

C．等腰梯形

D．正方形

四边形ABCD中，对角线AC、BD相交于点O，给出下列四组条件：①AB∥CD，AD∥BC；②AB=CD，AD=BC；③AO=CO，BO=DO；④AB∥CD，AD=BC．其中一定能判定这个四边形是平行四边形的条件有    
A．1组             B．2组             C．3组             D．4组

已知菱形ABCD的边长为6，∠A=60⁰，如果点P是菱形内一点，且PB="PD" =2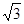，那么AP的长为         .

如图，在直角坐标系中，点的坐标为，点在直线上运动，点、、分别为、、的中点，其中是大于零的常数.
（1）请判断四边形的形状，并证明你的结论；
（2）试求四边形的面积与的关系式；
（3）设直线与轴交于点，问：四边形能不能是矩形？若能，求出的值；若不能，说明理由.

如图，正方形ABCD是⊙O的内接正方形，点P是⌒CD上不同于点C的任意一点，则∠BPC的度数是_____________度.

如图，在直角梯形中，AB∥CD；⊥动点从点出发，沿，运动至点停止．设点运动的路程为，的面积为，如果关于的函数图象如图所示，则的面积是（   ）

A．3

B．4

C．5

D．6

如图，梯形ABCD中，AD∥BC，∠BAD=90°，CE⊥AD于点E，AD=4cm，BC=2cm，AB=3cm.从初始时刻开始，动点P、Q分别从点A、B同时出发，运动速度均为1 cm/s，动点P沿A→B→C→E的方向运动，到点E停止；动点Q沿B→C→E→D的方向运动，到点D停止.设运动时间为s，PAQ的面积为y cm².（这里规定：线段是面积为0的三角形)解答下列问题：

（1）当x=" 2" s时，y=________cm²;当= s时，y=________cm²；
（2）当动点P在线段BC上运动，即3 ≤ x ≤ 5时，求y与之间的函数关系式，并求出时的值；
（3）当动点P在线段CE上运动，即5 < x ≤ 8 时，求y与之间的函数关系式；
（4）直接写出在整个运动过程中，使PQ与四边形ABCE的对角线平行的所有x的值．

如图，正方形ABCD中，AB=4，E是BC的中点，点P是对角线AC上一动点，则PE+PB的最小值为     ．