[吉林]2011-2012学年吉林省东丰县八年级上学期期末考试数学试卷
若点(-4,y1)、(2,y2)都在直线y=-3x+5上,则y1 y2
(填“>”、“=”或“<”).
将图(甲)中阴影部分的小长方形变换到图(乙)位置,根据两个图形的面积关系得到的数学公式是 .
如图所示,函数y1=|x|和 的图象相交于(-1,1),(2,2)两点.当
的图象相交于(-1,1),(2,2)两点.当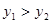 时,x的取值范围是 .
时,x的取值范围是 .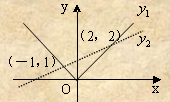
如图,在下列条件中,不能判断△ABD≌△BAC的条件是( ) 
| A.∠BAD=∠ABC,∠ABD=∠BAC | B.AD=BC,BD=AC |
| C.BD=AC,∠BAD=∠ABC | D.∠D=∠C,∠BAD=∠ABC |
如图,已知函数y=ax+y和y=kx的图象交于点P,则二元一次方程组 的解是( )
的解是( )
A. |
B. |
C. |
D. |

如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为 cm的正方形
cm的正方形 ,剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积( )
,剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积( )
A. |
B. |
C. |
D. |
如图,在等腰△ABC中,∠BAC=120º,DE是AC的垂直平分线,线段DE=1cm,则BD的长为( )
| A.3cm | B.4cm | C.6cm | D.8cm |

如图,A,B两点的坐标分别是(2, ),(3,0)
),(3,0)
(1)求△OAB的面积;
(2)将△OAB向下平移 个单位,画出平移后的图形,并写出所得的三角形的三个顶点的坐标。
个单位,画出平移后的图形,并写出所得的三角形的三个顶点的坐标。
如图,AD是ΔABC的角平分线,DE AB,DF
AB,DF AC,垂足分别是点E,F,连结EF,交AD于点G,求证:AD⊥EF
AC,垂足分别是点E,F,连结EF,交AD于点G,求证:AD⊥EF
小聪和小明沿同一条路同时从学校出发到图书馆查阅资料,学校与图书馆的路程是4千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达图书馆,图中折线O-A-B-C和线段OD分别表示两人离学校的路程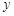 (千米)与所经过的时间
(千米)与所经过的时间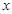 (分钟)之间的函数关系,请根据图象回答下列问题:
(分钟)之间的函数关系,请根据图象回答下列问题:
(1)小聪在图书馆查阅资料的时间为 分钟,小聪返回学校的速度为 千米/分钟.
(2)请你求出小明离开学校的路程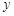 (千米)与所经过的时间
(千米)与所经过的时间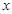 (分钟)之间的函数关系;
(分钟)之间的函数关系;
(3)当小聪与小明迎面相遇时,他们离学校的路程是多少千米?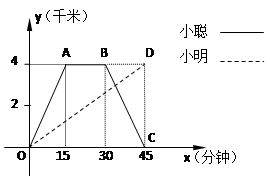
下面是某同学对多项式 进行因式分解的过程.
进行因式分解的过程.
解:设
原式= (第一步)
(第一步)
= (第二步)
(第二步)
= (第三步)
(第三步)
= (第四步)
(第四步)
请问:
(1)该同学因式分解的结果是否彻底?____________.(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果____________________________
(2)请你模仿以上方法尝试对多项式 进行因式分解.
进行因式分解.
如图,直线 与
与 轴负半轴、
轴负半轴、 轴正半轴分别交于A、B两点,正比例函数
轴正半轴分别交于A、B两点,正比例函数 的图像与直线AB交于点Q,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM =10,BN =3,
的图像与直线AB交于点Q,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM =10,BN =3,
(1)求A、B两点的坐标;(用b表示)
(2)图中有全等的三角形吗?若有,请找出并说明理由。
(3)求MN的长.
如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(-4,0),点B的坐标为(0,b)(b>0). P是直线AB上的一个动点,作PC⊥x轴,垂足为C.记点P关于y轴的对称点为P'(点 P'不在y轴上),连结P P', P'A,P'C.设点P的横坐标为a.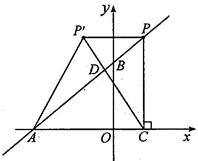
(1) 当b=3时,求直线AB的解析式;
(2) 在(1)的条件下,若点P'的坐标是(-1,m),求m的值;
(3) 若点P在第一像限,是否存在a ,使△P'CA为等腰直角三角形?若存在,请求出所有满足要求的a的值;若不存在,请说明理由.
 的图像经过第 象限.
的图像经过第 象限. ,则
,则 = .
= . ,且∠O=72°,∠C=28°则∠OAD= .
,且∠O=72°,∠C=28°则∠OAD= .
 是一个完全平方式,则常数k的值为 .
是一个完全平方式,则常数k的值为 . 可化为
可化为 ,则
,则 的值是 .
的值是 .




 +
+ -
-

 ,其中
,其中 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号