如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(-4,0),点B的坐标为(0,b)(b>0). P是直线AB上的一个动点,作PC⊥x轴,垂足为C.记点P关于y轴的对称点为P'(点 P'不在y轴上),连结P P', P'A,P'C.设点P的横坐标为a.
(1) 当b=3时,求直线AB的解析式;
(2) 在(1)的条件下,若点P'的坐标是(-1,m),求m的值;
(3) 若点P在第一像限,是否存在a ,使△P'CA为等腰直角三角形?若存在,请求出所有满足要求的a的值;若不存在,请说明理由.
推荐套卷
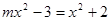 (
( )
)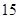 千米到李庄,甲比乙每小时多走
千米到李庄,甲比乙每小时多走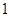 千米,结果比乙早到半小时.问二人每小时各走几千米?
千米,结果比乙早到半小时.问二人每小时各走几千米?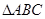 中,点
中,点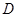 在边
在边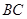 上,
上,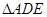 为等边三角形,且点
为等边三角形,且点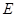 与点
与点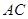 的两侧,点
的两侧,点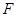 在
在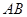 上(不与
上(不与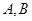 重合)且
重合)且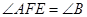 ,
,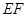 与
与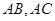 分别相交于点
分别相交于点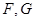 .
.
 是平行四边形
是平行四边形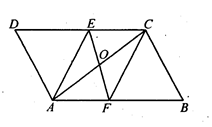
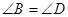
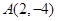 、
、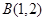 .
.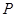 在这个一次函数图像上且它的纵坐标为
在这个一次函数图像上且它的纵坐标为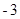 ,求点
,求点 粤公网安备 44130202000953号
粤公网安备 44130202000953号