初中数学圆内接四边形的性质试题

如图，E是矩形ABCE的边BC上一点，EF⊥AE，EF分别交AC、CD于点M、F，BG⊥AC，垂足为G，BG交AE于点H。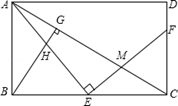

（1）求证：△ABE∽△ECF；
（2）找出与△ABH相似的三角形，并证明；
（3）若E是BC中点，BC=2AB，AB=2，求EM的长。

如图，□ABCD中，E是AB中点，F在AD上，且AF＝FD，EF交AC于G，则AG︰AC＝______．

如图，Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的，连结CC′交斜边于点E，CC′的延长线交BB′于点F。

（1）若AC=3，AB=4，求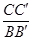
（2）证明：△ACE∽△FBE；
（3）设∠ABC=，∠CAC′=，试探索、满足什么关系时，△ACE与△FBE是全等三角形，并说明理由。

已知，在△ABC中，∠BAC=90º， AB=AC，点D为直线BC上一动点（点D不与B、C重合）.以AD为边作正方形ADEF．连接CF.

（1）如图1，当点D在线段BC上时，求证：①CF＝BD；②CF⊥BD；
（2）如图2，当点D在线段BC的延长线上时，其它条件不变，线段CF与BD的上述关系是否还成立？请直接写出结论即可（不必证明）；
（3）如图3，当点D在线段BC的反向延长线上，且点A、F在直线BC的两侧，其它条件不变，线段CF与BD的上述关系是否还成立？若成立，请证明你的结论；若不成立，请说明理由.

如图，将边长为2的正方形纸片ABCD折叠，使点B 落在CD上，落点记为E（不与点C，D重合），点A落在点F处，折痕MN交AD于点M，交BC于点N．若，则BN的长是   ，的值等于     ；若（，且为整数），则的值等于       （用含的式子表示）．

阅读理解：如图（1），已知直线m∥n，A、B 为直线n上两点，C、D为直线m上两点，容易证明：△ABC的面积=△ABD的面积．根据上述内容解决以下问题：

已知正方形ABCD的边长为4，G是边CD上一点，以CG为边作正方形GCEF．

（1）如图（2），当点G与点D重合时，△BDF的面积为      ；
（2）如图（3），当点G是CD的中点时，△BDF的面积为      ；
（3）如图（4），当CG = a时，则△BDF的面积为      ，并说明理由；
探索应用：小张家有一块正方形的土地如图（5），由于修建高速公路被占去一块三角形BCP区域．现决定在DP右侧补给小张一块土地，补偿后土地变为四边形ABMD，要求补偿后的四边形ABMD的面积与原来形正方形ABCD的面积相等且M在射线BP上，请你在图中画出M点的位置，并简要叙述做法．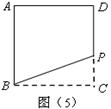

探究：如图（1），在□ABCD的形外分别作等腰直角△ABF和等腰直角△ADE，∠FAB=∠EAD=90⁰，连接AC，EF。在图中找一个与△FAE全等的三角形，并加以证明。
应用：以□ABCD的四条边为边，在其形外分别作正方形，如图（2），连接EF，GH，IJ，KL。若□ABCD的面积为6，则图中阴影部分四个三角形的面积和为____________.

推广：以□ABCD的四条边为矩形长边，在其形外分别作长与宽之比为矩形，如图（3），连接EF，GH，IJ，KL。若图中阴影部分四个三角形的面积和为12，求□ABCD的面积？

（1）操作发现：

如图，矩形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE，且点在G矩形ABCD内部．小明将BG延长交DC于点F，认为GF=DF，你同意吗？说明理由．
（2）问题解决:保持（1）中的条件不变，若DC=2DF，求值．
（3）类比探究: 保持（1）中的条件不变，若DC=n.DF，求的值（直接写出答案）

如图，在平行四边形ABCD中，E、F为BC上两点，且BE=CF,AF=DE.

（1）找出图中一对全等的三角形，并证明；
（2）求证：四边形ABCD是矩形．

如图，用纸折出黄金分割点：裁一张正方的纸片ABCD，先折出BC的中点E，再折出线段AE，然后通过折叠使EB落到线段EA上，折出点B的新位置B′，因而EB′=EB．类似地，在AB上折出点B″使AB″=AB′．这时B″就是AB的黄金分割点．请你证明这个结论．

在直线l上依次摆放着七个正方形(如图所示)。已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是S₁、S₂、S₃、S₄，则S₁＋S₂＋S₃＋S₄的值为（　　）

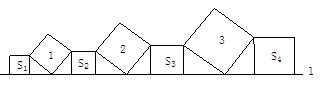
A．6

B．5

C．4

D．3

（1）如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE．求证：CE＝CF；
（2）如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠ECG＝45°，请你利用（1）的结论证明：．
（3）运用（1）、（2）解答中所积累的经验和知识，完成下题：
如图3，在直角梯形ABCG中，AG∥BC（BC＞AG），∠B＝90°，AB＝BC=6，E是AB上一点，且∠ECG＝45°，BE＝2．求△ECG的面积．

如图，正方形ABCD的边长为1，点E是AD边上的动点，从点A沿AD向D运动，以BE为边，在BE的上方作正方形BEFG，连接CG。请探究：

（1）线段AE与CG是否相等？请说明理由。
（2）若设AE=x，DH=y，当x取何值时，y最大？
（3）连接BH，当点E运动到AD的何位置时，△BEH∽△BAE？

如图①，正方形 ABCD中，点A、B的坐标分别为（0，10），（8，4），点C在第一象限．动点P在正方形 ABCD的边上，从点A出发沿A→B→C→D匀速运动，同时动点Q以相同速度在x轴正半轴上运动，当P点到达D点时，两点同时停止运动，设运动的时间为t秒．

（1）当P点在边AB上运动时，点Q的横坐标（长度单位）关于运动时间t（秒）的函数图象如图②所示，请直接写出点Q开始运动时的坐标及点P运动速度；
（2）求正方形边长及顶点C的坐标；
（3）在（1）中当t为何值时，△OPQ的面积最大，并求此时P点的坐标；
（4）如果点P、Q保持原速度不变，当点P沿A→B→C→D匀速运动时，OP与PQ能否相等，若能，直接写出所有符合条件的t的值；若不能，请说明理由．

如图，在直角梯形ABCD中，AD∥BC，∠B=90°，AD=24cm，AB=8cm，BC=26cm，动点P从A开始沿AD边向D以1cm/s的速度运动；动点Q从点C开始沿CB边向B以3cm/s的速度运动．P、Q分别从点A、C同时出发，当其中一点到达端点时，另外一点也随之停止运动，设运动时间为ts．

（1）当t为何值时，四边形PQCD为平行四边形？
（2）当t为何值时，四边形PQCD为等腰梯形？
（3）当t为何值时，四边形PQCD为直角梯形？