（1）操作发现：
如图，矩形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE，且点在G矩形ABCD内部．小明将BG延长交DC于点F，认为GF=DF，你同意吗？说明理由．
（2）问题解决:保持（1）中的条件不变，若DC=2DF，求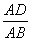
值．
（3）类比探究: 保持（1）中的条件不变，若DC=n.DF，求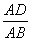的值（直接写出答案）
相关知识点
推荐套卷
（1）操作发现：
如图，矩形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE，且点在G矩形ABCD内部．小明将BG延长交DC于点F，认为GF=DF，你同意吗？说明理由．
（2）问题解决:保持（1）中的条件不变，若DC=2DF，求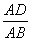值．
（3）类比探究: 保持（1）中的条件不变，若DC=n.DF，求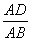的值（直接写出答案）
粤公网安备 44130202000953号