初中数学圆内接四边形的性质试题

已知：如图所示的一张矩形纸片，将纸片折叠一次，使点与重合，再展开，折痕交边于，交边于，分别连接和．

（１）求证：四边形是菱形.
（２）若，△的面积为，求△的周长.
（３）在线段上是否存在一点，使得？若存在，请说明点的位置，并予以证明；若不存在，请说明理由．

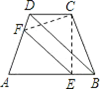
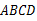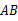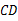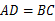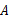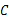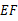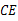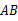如图，四边形为一梯形纸片，∥，．翻折纸片，使点与点重合，折痕为．已知⊥，试说明：∥.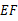

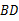四边形是大家最熟悉的图形之一，我们已经发现了它的许多性质.只要善于观察、乐于探索，我们还会发现更多的结论.

（1）四边形一条对角线上任意一点与另外两个顶点的连线，将四边形分成四个三角形（如图①），其中相对的两对三角形的面积之积相等.你能证明这个结论吗？试试看.
已知：在四边形ABCD中，O是对角线BD上任意一点（如图①）；
求证：.
证明：
（2）在三角形中（如图②），你能否归纳出类似的结论？若能，写出你猜想的结论，并证明;若不能，请说明理由.

如图，已知线段AB=10，AC=BD=2，点P是CD上一动点，分别以AP、PB为边向上、向下作正方形APEF和PHKB，设正方形对角线的交点分别为O₁、O₂，当点P从点C运动到点D时，线段O₁O₂中点G的运动路径的长是_____．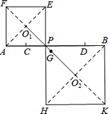

如图,在矩形ABCD中,点O是边AD上的中点,点E是边BC上的一个动点,延长EO到F,使得OE=OF.

（1）当点E运动到什么位置时,四边形AEDF是菱形？（直接写出答案）
（2）若矩形ABCD的周长为20,四边形AEDF的面积是否存在最大值？如果存在,请求出最大值;如果不存在,请说明理由．
（3）若AB=,BC=,当.满足什么条件时,四边形AEDF能成为一个矩形？（不必说明理由）

如图，梯形ABCD中，AD//BC，AD=2，BC=8，AC=6，BD=8，则梯形ABCD的面积是       .

如图，矩形ABCD的对角线相交于点O，DE∥CA，AE∥BD．

（1）求证：四边形AODE是菱形；
（2）若将题设中“矩形ABCD”这一条件改为“菱形ABCD”，其余条件不变，则四边形AODE的形状是什么？说明理由．

如图1，△ABC是等腰直角三角形，∠BAC=90°，AB=AC，四边形ADEF是正方形，D、F分别在AB、AC边上，此时BD=CF，BD⊥CF成立．

（1）当正方形ADEF绕点A逆时针旋转θ（0°＜θ＜90°）时，如图2，BD=CF成立吗？若成立，请证明；若不成立，请说明理由．

（2）当正方形ADEF绕点A逆时针旋转45°时，如图3，延长BD交CF于点G．

①求证：BD⊥CF；
②当AB=4，AD=时，求线段FG的长．

阅读下列材料：
如图1，在梯形ABCD中，AD∥BC，点M、N分别在边AB、BC上，且MN∥AD，记AD=a，BC=b，若，则有结论：。

请根据以上结论，解答下列问题：

如图2，3，BE、CF是△ABC的两条角平分线，过EF上一点P分别作△ABC三边的垂线段PP₁、PP₂、PP₃，交BC于点P₁，交AB于点P₂，交AC于点P₃。
（1）若点P为线段EF的中点，求证：PP₁=PP₂＋PP₃；
（2）若点P在线段EF上任意位置时，试探究PP₁、PP₂、PP₃的数量关系，给出证明。

如图，正方形ABCD的边长是3，点P是直线BC上一点，连接PA，将线段PA绕点P逆时针旋转90°得到线段PE，在直线BA上取点F，使BF=BP，且点F与点E在BC同侧，连接EF，CF．

（1）如图①，当点P在CB延长线上时，求证：四边形PCFE是平行四边形；
（2）如图②，当点P在线段BC上时，四边形PCFE是否还是平行四边形，说明理由；
（3）在（2）的条件下，四边形PCFE的面积是否有最大值？若有，请求出面积的最大值及此时BP长；若没有，请说明理由．

已知：如图，在ABCD中，AE⊥BC，垂足为E，CE=CD，点F为CE的中点，点G为CD上的一点，连接DF、EG、AG，∠1=∠2。

（l）若CF=2，AE=3，求BE的长；
（2）求证：。

已知，如图①，在平行四边形ABCD中，AB=12，BC=6，AD⊥BD。以AD为斜边在平行四边形ABCD的内部作Rt△AED，∠EAD=30⁰，∠AED=90⁰。

（1）求△AED的周长；
（2）若△AED以每秒2个长度单位的速度沿DC向右平行移动，得到△A₀E₀D₀，当A₀D₀与BC重合时停止移动。设移动时间为t秒，△A₀E₀D₀与△BDC重叠部分的面积为S，请直接写出S与t之间的函数关系式，并写出t的取值范围；
（3）如图②，在（2）中，当△AED停止移动后得到△BEC，将△BEC绕点C按顺时针方向旋转，在旋转过程中，B的对应点为B₁，E的对应点为E₁，设直线B₁E₁与直线BE交于点P、与直线CB交于点Q。是否存在这样的，使△BPQ为等腰三角形？若存在，求出的度数；若不存在，请说明理由。

如图，在矩形ABCD中，E、F分别是边AB、CD上的点，AE=CF，连接EF，BF，EF与对角线AC交于O点，且BE=BF，∠BEF=2∠BAC。

（1）求证：OE=OF；
（2）若BC=，求AB的长。

如图，在Rt△ABC中，∠B=90°，AC=60cm，∠A=60°，点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（0＜t≤15）．过点D作DF⊥BC于点F，连接DE，EF．

（1）求证：AE=DF；
（2）四边形AEFD能够成为菱形吗？如果能，求出相应的t值，如果不能，说明理由；
（3）当t为何值时，△DEF为直角三角形？请说明理由．

如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC．设MN交∠ACB的平分线于点E，交∠ACB的外角平分线于点F．

（1）求证：OE=OF；
（2）若CE=12，CF=5，求OC的长；
（3）当点O在边AC上运动到什么位置时，四边形AECF是矩形？并说明理由．