[山东]2013届山东省德州市九年级第一次模拟考试数学试卷
由两个紧靠在一起的圆柱组成的几何体如图所示,则它的俯视图是( )
| A.两个内切的圆 | B.两个相交的圆 | C.两个外切的圆 | D.两个外离的圆 |
不等式组 的解集是( )
的解集是( )
| A.x > -1 | B.-1< x < 2 | C.x < 2 | D.x < -1或x > 2 |
如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个钝角为100° 的菱形,剪口与折痕所成的角的度数应为( )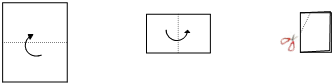
| A.25°或50° | B.20°或50° | C.40°或50° | D.40°或80° |
如图,为了测量某棵树的高度,小明用长为2m的竹竿作测量工具,移动竹竿,使竹竿顶端、树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距6m,与树相距15m,则树的高度为 ( ) 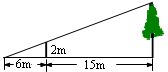
| A.9m | B.7m | C.4m | D.5m |
四名运动员参加了射击预选赛,他们的成绩的平均环数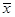 及方差S2如下表所示:
及方差S2如下表所示:
| |
甲 |
乙 |
丙 |
丁 |
 |
8.3 |
9.2 |
9.2 |
8.5 |
| S2 |
1 |
1 |
1.1 |
1.7 |
如果选出一个成绩较好且状态稳定的人去参赛,那么应选( )
A.甲 B.乙 C.丙 D.丁
如图,在△ABC中,点E 、D、F分别在边AB、BC、CA上,且DE∥AC,DF∥AB.下列说法中错误的是( )

A.四边形AEDF是平行四边形
B.如果∠BAC="90" º,那么四边形AEDF是矩形
C.如果AD⊥BC,那么四边形AEDF是正方形
D.如果AD平分∠BAC,那么四边形AEDF是菱形
二次函数 的图象如图所示,在下列说法中:
的图象如图所示,在下列说法中:
① 0;②
0;② ;③
;③ ;
;
④当 时,
时, 随着
随着 的增大而增大.正确的说法个数是( )
的增大而增大.正确的说法个数是( )
| A.1 | B.2 | C.3 | D.4 |
如图是一个由正方形ABCD和半圆O组成的封闭图形,点O是圆心.点P从点A出发,沿弧AB、线段BC、线段CD和线段DA匀速运动,到达终点A.运动过程中OP扫过的面积(s)随时间(t)变化的图象大致是( ) 

2012年德州市参加中考人数约为39400人.39400用科学计数法表示为_____________.
如图,矩形ABCD中,E为DC的中点,AD: AB=  :2,CP:BP=1:2,连接EP并延长,交AB的延长线于点F,AP、BE相交于点O.下列结论:①EP平分∠CEB;②△EBP∽△EFB;③△ABP∽△ECP;④AO
:2,CP:BP=1:2,连接EP并延长,交AB的延长线于点F,AP、BE相交于点O.下列结论:①EP平分∠CEB;②△EBP∽△EFB;③△ABP∽△ECP;④AO AP=OB2.其中正确的序号是_______________.(把你认为正确的序号都填上)
AP=OB2.其中正确的序号是_______________.(把你认为正确的序号都填上)
如图,在平面直角坐标系中,∠AOB=30°,点A坐标为(2,0).过A作 AA1⊥OB,垂足为点A1;过点A1作A1A2⊥x轴,垂足为点A2;再过点A2作A2A3⊥OB,垂足为点A3;再过点A3作A3A4⊥x轴,垂足为点A4; ;这样一直作下去,则A2013的纵坐标为 .
为更好地宣传“开车不喝酒,喝酒不开车”的驾车理念,某市一家报社设计了如下的调查问卷(单选).在随机调查了本市全部8000名司机中的部分司机后,统计整理并制作了如下的统计图:


根据以上信息解答下列问题:
(1)补全条形统计图,并计算扇形统计图中m=________;
(2)该市支持选项B的司机大约有多少人?
(3)若要从该市支持选项B的司机中随机选择100名,给他们发放“请勿酒驾”的提醒标志,则支持该选项的司机王明被选中的概率是多少?
如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.
(1)求证:直线BF是⊙O的切线;
(2)若点D,点E分别是弧AB的三等分点,当AD=5时,求BF的长.
在市政府实施市容市貌工程期间,某中学在教学楼前铺设小广场地面.其图案设计如图1,正方形小广场地面的边长是40m,中心建一直径为20m的圆形花坛,四角各留一个边长为10m的小正方形花坛,种植高大树木.图中其余部分铺设广场砖.
(1)请同学们帮助计算铺设广场砖部分的面积 (
( 取3);
取3);
(2)某施工队承包铺设广场砖的任务,计划在一定时间内完成,按计划工作一天后,由于改进了铺设工艺,每天比原计划多铺60 ,结果提前3天完成了任务,原计划每天铺设多少
,结果提前3天完成了任务,原计划每天铺设多少 ?
?
(3)如图2表示广场中心圆形花坛的平面图,准备在圆形花坛内种植6种不同颜色的花卉,为了美观,要使同色花卉集中在一起,并且各花卉的种植面积相等.请你帮助设计一种方案,画在图2上.(不必说明方案,不写作法,保留作图痕迹)
(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠ECG=45°,请你利用(1)的结论证明: .
.
(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCG中,AG∥BC(BC>AG),∠B=90°,AB=BC=6,E是AB上一点,且∠ECG=45°,BE=2.求△ECG的面积.
已知:如图,在Rt△ABC中,∠ACB=90°,BC="3" ,tan∠BAC= ,将∠ABC对折,使点C的对应点H恰好落在直线AB上,折痕交AC于点O,以点O为坐标原点,AC所在直线为x轴建立平面直角坐标系
,将∠ABC对折,使点C的对应点H恰好落在直线AB上,折痕交AC于点O,以点O为坐标原点,AC所在直线为x轴建立平面直角坐标系
(1)求过A、B、O三点的抛物线解析式;
(2)若在线段AB上有一动点P,过P点作x轴的垂线,交抛物线于M,设PM的长度等于d,试探究d有无最大值,如果有,请求出最大值,如果没有,请说明理由.
(3)若在抛物线上有一点E,在对称轴上有一点F,且以O、A、E、F为顶点的四边形为平行四边形,试求出点E的坐标.



 =
=
 等于( )
等于( )




 的两个实数根,则
的两个实数根,则 为( ).
为( ). ,则(-2)
,则(-2) (-3)= .
(-3)= . 与直线
与直线 相交于O(0,0)和A(3,2)两点,则不等式
相交于O(0,0)和A(3,2)两点,则不等式 的解集为 .
的解集为 .
 ,其中a=
,其中a= .
. 的图象上.
的图象上. 时,求
时,求 的值;
的值; 时,求
时,求 粤公网安备 44130202000953号
粤公网安备 44130202000953号