如图,在梯形ABCD中,AD∥BC,AB=5,AD=6,DC=4,∠C=45º. 动点M从B点出发沿线段BC以每秒1个单位长度的速度向终点C运动;动点N同时从C点出发沿C→D→A运动,在CD上的速度为每秒个单位长度,在DA上的速度为每秒1个单位长度,当其中一个点到达终点是另一个点也随之停止运动.设运动的时间为t秒.
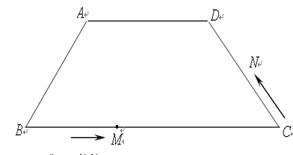
(1)求BC的长.
(2)当四边形ABMN是平行四边形时,求t的值.
(3)试探究:t为何值时,△ABM为等腰三角形.
相关知识点
推荐套卷
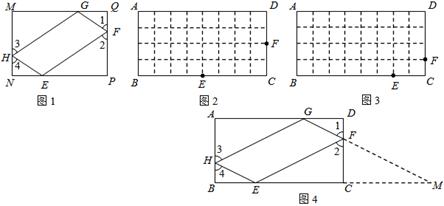
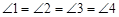 ,则称四边形EFGH为矩形MNPQ的反射四边形.图2,图3,图4中,四边形ABCD为矩形,且
,则称四边形EFGH为矩形MNPQ的反射四边形.图2,图3,图4中,四边形ABCD为矩形,且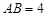 ,
,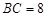 .
.
 (时),两车之间的距离为
(时),两车之间的距离为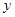 (千米),图中的折线表示从两车出发至快车到达乙地过程中
(千米),图中的折线表示从两车出发至快车到达乙地过程中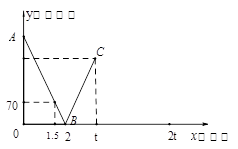
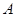 型车和1辆
型车和1辆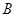 型车装满货物一次可运货10吨;用1辆
型车装满货物一次可运货10吨;用1辆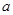 辆,
辆,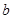 辆,一次运完,且恰好每辆车都装满货物.根据以上信息,解答下列问题:
辆,一次运完,且恰好每辆车都装满货物.根据以上信息,解答下列问题: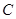 为线段
为线段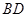 上一动点,分别过点
上一动点,分别过点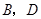 作
作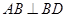 ,
,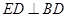 ,连接
,连接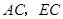 .已知
.已知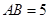 ,
,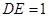 ,
,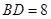 ,设
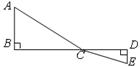
,设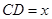 .
.
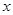 的代数式表示
的代数式表示 的长;
的长;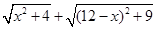 的最小值.
的最小值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号