[江苏]2011-2012学年江苏省九年级上学期第一次学情调研考试数学试卷
下列图形中,既是轴对称图形,又是中心对称图形的个数是( )
| A.1个 | B.2个 | C.3个 | D.4个 |
已知四边形 ,有以下四个条件:①
,有以下四个条件:① ∥
∥ ;②
;② ;③
;③ ∥
∥ ;④
;④ .从这四个条件中任选两个,能使四边形
.从这四个条件中任选两个,能使四边形 成为平行四边形的选法共有( )
成为平行四边形的选法共有( )
| A.6种 | B.5种 | C.4种 | D.3种 |
下列说法中,错误的是( )
| A.平行四边形的对角线互相平分 | B.矩形的对角线互相垂直 |
| C.菱形的对角线互相垂直平分 | D.等腰梯形的对角线相等 |
下列四边形中,两条对角线一定不相等的是( )
| A.正方形 | B.矩形 | C.等腰梯形 | D.直角梯形 |
下列说法中:①位似图形一定是相似图形;②相似图形一定是位似图形;③两个位似图形若全等,则位似中心在两个图形之间;④若五边形ABCDE与五边形A'B'C'D'E'位似,则在五边形中连线组成的△ABC与△A'B'C'也是位似的。正确的个数是( )
| A.1 | B.2 | C.3 | D.4 |
如图,小区的一角有一块形状为等腰梯形的空地,为了美化小区,社区居委会计划在空地上建一个四边形的水池,使水池的四个顶点恰好在梯形各边的中点上,则水池的形状一定是( )
| A.等腰梯形 | B.矩形 | C.菱形 | D.正方形 |
如图,四边形ABCD的对角线互相平分,若要使它成为矩形,需要添加的条件是( )
A. |
B. |
C. |
D. |
如图,在方格纸上 是由
是由 绕定点
绕定点 顺时针旋转得到的.如果用(2,1)表示方格纸上
顺时针旋转得到的.如果用(2,1)表示方格纸上 点的位置,(1,2)表示
点的位置,(1,2)表示 点的位置,那么点
点的位置,那么点 的位置为( )
的位置为( )
| A.(5,2) | B.(2,5) | C.(2,1) | D.(1,2) |
如图,在□ABCD中, 是
是 的中点,且
的中点,且 ,有下列结论:①.两三角形面积
,有下列结论:①.两三角形面积 ②.
②. ③.四边形
③.四边形 是等腰梯形 ④.
是等腰梯形 ④. 其中不正确的是_________________.
其中不正确的是_________________.
如图,在平面直角坐标系中,将线段OC向右平移到AB,且OA=OC,形成菱形 的顶点
的顶点 的坐标是(3,4),则顶点
的坐标是(3,4),则顶点 、
、 的坐标分别是_________________..
的坐标分别是_________________..
如上图,在一块形状为直角梯形的草坪中,修建了一条由 →
→ →
→ →
→ 的小路(
的小路( 、
、 分别是
分别是 、
、 中点).极少数同学为了走“捷径”,沿线段
中点).极少数同学为了走“捷径”,沿线段 行走,破坏了草坪,实际上他们仅少走了________米。
行走,破坏了草坪,实际上他们仅少走了________米。
如图所示,平行四边形 的周长是18cm,
的周长是18cm, <
< .对角线
.对角线 、
、 相交于点
相交于点 ,若
,若 与
与 的周长差是5cm,则边
的周长差是5cm,则边 的长是________ cm.
的长是________ cm. 
如图,已知矩形纸片ABCD,点E是AB的中点,点G是BC上的一点,∠BEG>60°,现沿直线EG将纸片折叠,使点B落在纸片上的点H处,连结AH,则与∠BEG相等的角的个数为_____个。
如图,在矩形ABCD中,AB=3,BC=5,过对角线交点O作OE⊥AC交AD于E,则AE的长是_____________.
如图,矩形纸片ABCD的边长AB=4,AD=2,将矩形纸片沿EF折叠,使点A与点C重合,折叠后在其一面着色(如图),着色部分的面积为______________.
如图,将边长为8 cm的正方形纸片ABCD折叠,使点D落在BC边中点E处,点A落在点F处,折痕为MN,则线段CN的长度为_________________.
如图,在边长为2 cm的正方形ABCD中,点Q为BC边的中点,点P为对角线AC上一动点,连结PB、PQ,则△PBQ周长的最小值为________cm(结果不取近似值).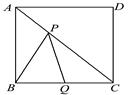
如图,在四边形 中,E、F、G、H分别是
中,E、F、G、H分别是 、
、 、
、 、
、 的中点.
的中点.
(1)请判断四边形 的形状.并说明为什么?
的形状.并说明为什么?
(2)若使四边形 为正方形,那么四边形
为正方形,那么四边形 的对角线应具有怎样的性质?
的对角线应具有怎样的性质?
如图,在 和
和 中,
中, ,
, ,
, >
> ,
, ,点
,点 、
、 、
、 在直线
在直线 上,
上,
(1)按下列要求画图(保留画图痕迹):
①画出点 关于直线
关于直线 的对称点
的对称点 ,连接
,连接 、
、 ;
;
②以点 为旋转中心,将(1)中所得
为旋转中心,将(1)中所得 按逆时针方向旋转,使得
按逆时针方向旋转,使得 旋转后的线段
旋转后的线段
 与
与 重合,得到
重合,得到 (A),画出
(A),画出 .
.
(2)解决下面问题:
①线段 和线段
和线段 的位置关系是 .并说明理由.
的位置关系是 .并说明理由.
②求∠ 的度数.
的度数.
如图,正方形ABCD绕点A逆时针旋转no后得到正方形AEFG,EF与CD交于点O.
(1)以图中已标有字母的点为端点连结两条线段(正方形的对角线除外),要求所连结的两条线段相交且互相垂直,并说明这两条线段互相垂直的理由;
(2)若正方形的边长为2cm,重叠部分(四边形AEOD)的面积为 cm2,求旋转的角度n.
cm2,求旋转的角度n.
如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
(3)在(2)的条件下,当△ABC满足什么条件时,四边形AECF是正方形?
如图所示,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连结AE、CF.
(1)求证:AF=CE;
(2)若AC=EF,试判断四边形AFCE是什么样的四边形,并证明你的结论
已知:如图,在正方形 中,点
中,点 、
、 分别在
分别在 和
和 上,
上, .
.
(1)求证: ;
;
(2)连接 交
交 于点
于点 ,延长
,延长 至点
至点 ,使
,使 ,连接
,连接 、
、 ,判断四边形
,判断四边形 是什么特殊四边形?并证明你的结论.
是什么特殊四边形?并证明你的结论.
 中,
中, ∥
∥ ,
, ,
, ,
, ,则梯形
,则梯形
 、
、 是□
是□ 的对角线
的对角线 上的两点,
上的两点, .
. ;(2)
;(2) ∥
∥ .
.
 中,
中, ,
, 为
为 中点,四边形
中点,四边形 是平行四边形.求证:四边形
是平行四边形.求证:四边形 是矩形.
是矩形.
 中,
中, ∥
∥ ,
, ,
, 为
为
 ≌
≌ .(2)若
.(2)若 平分
平分 ,且
,且 ,求
,求 的长.
的长.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号