如图,在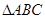 和
和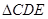 中,
中,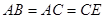 ,
,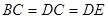 ,
,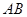 >
>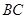 ,
,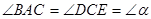 ,点
,点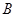 、
、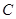 、
、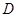 在直线
在直线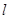 上,
上,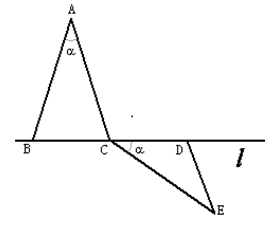
(1)按下列要求画图(保留画图痕迹):
①画出点 关于直线
关于直线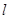 的对称点
的对称点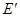 ,连接
,连接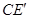 、
、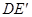 ;
;
②以点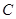 为旋转中心,将(1)中所得
为旋转中心,将(1)中所得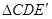 按逆时针方向旋转,使得
按逆时针方向旋转,使得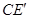 旋转后的线段
旋转后的线段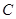
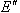 与
与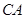 重合,得到
重合,得到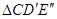 (A),画出
(A),画出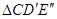 .
.
(2)解决下面问题:
①线段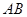 和线段
和线段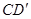 的位置关系是 .并说明理由.
的位置关系是 .并说明理由.
②求∠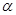 的度数.
的度数.
相关知识点
推荐套卷
如图,在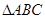 和
和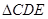 中,
中,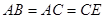 ,
,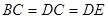 ,
,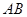 >
>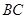 ,
,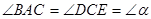 ,点
,点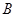 、
、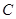 、
、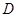 在直线
在直线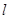 上,
上,
(1)按下列要求画图(保留画图痕迹):
①画出点 关于直线
关于直线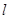 的对称点
的对称点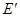 ,连接
,连接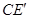 、
、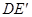 ;
;
②以点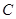 为旋转中心,将(1)中所得
为旋转中心,将(1)中所得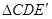 按逆时针方向旋转,使得
按逆时针方向旋转,使得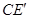 旋转后的线段
旋转后的线段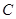
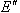 与
与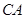 重合,得到
重合,得到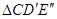 (A),画出
(A),画出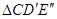 .
.
(2)解决下面问题:
①线段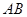 和线段
和线段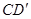 的位置关系是 .并说明理由.
的位置关系是 .并说明理由.
②求∠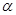 的度数.
的度数.