[江苏]2006年初中毕业升学考试（江苏无锡卷）数学

－3的绝对值是　　　　，4的算术平方根是　　　　。

分解因式：　　　　　　　　。

温家宝总理在十届全国人大四次会议上谈到解决关于“三农”问题时说，2006年中央财政用于“三农”的支出将达到33 970 000万元，这个数据用科学记数法可表示为_____ 　　  万元。

点（2，－1）关于x轴的对称点的坐标为　　　　　。

函数中，自变量的取值范围是　　　；函数中，自变量的取值范围是　　　　　　　　。

函数的图象经过点（－l，），则＝　　　　　　　。

如图所示，图中的∠1＝　　　　º。

如图，点A、B、C、D在⊙O上，若∠C＝60º，则∠D＝　　　º，∠O＝　　　　º。

若一个多边形的每一个外角都等于40º，则这个多边形的边数是　　　　　　。

在一个不透明的口袋中装有3个红球、1个白球，它们除颜色不相同外，其余均相同．若把它们搅匀后从中任意摸出1个球，则摸到红球的概率是　　　　　　　。

据国家统计局5月23日发布的公告显示，2006年一季度GDP值为43390亿元，其中，第一、第二、第三产业所占比例如图所示。根据图中数据可知，今年一季度第—产业的GDP值约为　　　　　　亿元（结果精确到0.01）。

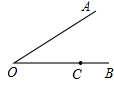
已知∠AOB＝30º，C是射线0B上的一点，且OC＝4。若以C为圆心，r为半径的圆与射线OA有两个不同的交点，则r的取值范围是　　　　　　。

在实数的原有运算法则中我们补充定义新运算“+”如下：
当a≥b时，a+b＝b²；当a＜b时，a+b＝a。
则当x＝2时，（1+x）·x－（3+x）的值为        
（“· ”和“－”仍为实数运算中的乘号和减号）。

下列各式中，与是同类根式的是（　　）

A．

B．

C．

D．

如图，O是原点，实数a、b、c在数轴上对应的点分别为A、B、C，则下列结论错误的是（　　）

A．a－b＞0      B．ab＜0        C．a＋b＜0      D．b（a－c）＞0

设—元二次方程x²－2x－4＝0的两个实根为x₁和x₂，则下列结论正确的是（　　）

在下面四个图案中，如果不考虑图中的文字和字母，那么不是轴对称图形的是（　　）

已知⊙O₁和⊙O₂的半径分别为2和5，圆心距O_lO₂＝3，则这两圆的位置关系是（　　）

现有边长相等的正三角形、正方形、正六进形、正八边形形状的地砖，如果选择其中的两钟铺满平整的地面，那么选择的两种地砖形状不能是（　　）

探索规律：根据下图中箭头指向的规律，从2004到2005再到2006，箭头的方向是（　　）

计算：º      

解不等式组：

已知：如图，ABCD中，∠BCD的平分线交AB于E，交DA的延长线于F。求证：AE＝AF。

甲、乙两人都想去买一本某种辞典，到书店后，发现书架上只有一本该辞典，于是两人都想把书让给对方先买，为此两人发生了“争执”。最后两人商定，用掷一枚各面分别标有数字1，2，3，4的正四面体骰子来决定谁先买。若甲赢，则乙买；若乙赢，则甲买。具体规则是：“每人各掷一次，若甲掷得的数字比乙大，则甲赢；若甲掷得的数字不比乙大，则乙赢”。
请你用“画树状图”的方法帮他们分析一下，这个规则对甲、乙双方是否公平？

（1）如图1，己知△ABC中，AB＞AC。试用直尺（不带刻度）和圆规在图l中过点A作一条直线l，使点C关于直线l的对称点在边AB上（不要求写作法，也不必说明理由，但要保留作图痕迹）。
（2）如图2，己知格点△ABC，请在图2中分别画出与△ABC相似的格点△A₁B₁C₁和格点△A₂B₂C₂，并使△A_lB_lC_l与△ABC的相似比等于2，而A₂B₂C₂与△ABC的相似比等于。（说明：顶点都在网格线交点处的三角形叫做格点三角形。友情提示：请在画出的三角形的项点处标上相对应的字母！）

姚明是我国著名的篮球运动员，他在2005－2006赛季NBA常规赛中表现非常优异。下面是他在这个赛季中，分期与“超音速队”和“快船队”各四场比赛中的技术统计。

（1）请分别计算姚明在对阵“超音速”和“快船”两队的各四场比赛中，平均每场得多少分？
（2）请你从得分的角度分析，姚明在与“超音速”和“快船”的比赛中，对阵哪一个队的发挥更稳定？
（3）如果规定“综合得分”为：平均每场得分×1＋平均每场篮板×1．5十平均每场失误×（－1.5），且综合得分越高表现越好，那么请你利用这种评价方法，来比较姚明在分别与“超音速”和“快船”的各四场比赛中，对阵哪一个队表现更好？

一商场计划到计算器生产厂家购进一批A、B两种型号的计算器。经过商谈，A型计算器单价为50元，100只起售，超过100只的超过部分，每只优惠20％；B型计算器单价为22元，150只起售，超过l50只的超过部分，每只优惠2元。如果商家计划购进计算器的总量既不少于700只，又不多于800只，且分别用于购买A、B这两种型号的计算器的金额相等，那么该商场至少需要准备多少资金？

如图，△ABC中，∠ACB＝90º，AC＝BC＝1，将△ABC绕点C逆时针旋转角α。（0º＜α＜90º）得到△A₁B₁C₁，连结BB₁.设CB₁交AB于D，A₁B₁分别交AB、AC于E、F。

（1）在图中不再添加其它任何线段的情况下，请你找出一对全等的三角形，并加以证明（△ABC与△A₁B₁C₁全等除外）；
（2）当△BB₁D是等腰三角形时，求α；
（3）当α＝60º时，求BD的长。

已知抛物线y＝ax²＋bx＋c（a＞0）的顶点是C（0，1），直线l：y＝－ax＋3与这条抛物线交于P、Q两点，与x轴、y轴分别交于点M和N。
（1）设点P到x轴的距离为2，试求直线l的函数关系式；
（2）若线段MP与PN的长度之比为3:1，试求抛物线的函数关系式。

图1是“口子窖”酒的一个由铁皮制成的包装底盒，它是一个无盖的六棱柱形状的盒子（如图2），侧面是矩形或正方形．经测量，底面六边形有三条边的长是9cm，有三条边的长是3cm，每个内角都是120º，该六棱校的高为3cm。现沿它的侧棱剪开展平，得到如图3的平面展开图。

（1）制作这种底盒时，可以按图4中虚线裁剪出如图3的模片。现有一块长为17.5cm、宽为16.5cm的长方形铁皮，请问能否按图4的裁剪方法制作这样的无盖底盒？并请你说明理由；
（2）如果用一块正三角形铁皮按图5中虚线裁剪出如图3的模片，那么这个正三角形的边长至少应为　　　　　　　　　　　　　cm。（说明：以上裁剪均不计接缝处损耗。）

如图，在等腰梯形ABCD中，AB∥DC，AB＝8cm，CD＝2cm，AD＝6cm。点P从点A出发，以2cm/s的速度沿AB向终点B运动；点Q从点C出发，以1cm/s的速度沿CD、DA向终点A运动（P、Q两点中，有一个点运动到终点时，所有运动即终止）．设P、Q同时出发并运动了t秒。

（1）当PQ将梯形ABCD分成两个直角梯形时，求t的值；
（2）试问是否存在这样的t，使四边形PBCQ的面积是梯形ABCD面积的一半？若存在，求出这样的t的值，若不存在，请说明理由。